[알고리즘] 오일러 피 함수(Euler’s phi Function)

오일러 피 함수

정의

오일러 피 함수(Euler’s phi(Totient) Function)는 주어진 양의 정수 n에 대해 n보다 작거나 같은 자연수 중에서 n과 서로소인 숫자의 개수를 나타내는 함수이다.

즉, n보다 작거나 같은 숫자 중 n과 최대공약수(GCD)가 1인 숫자의 개수이다.

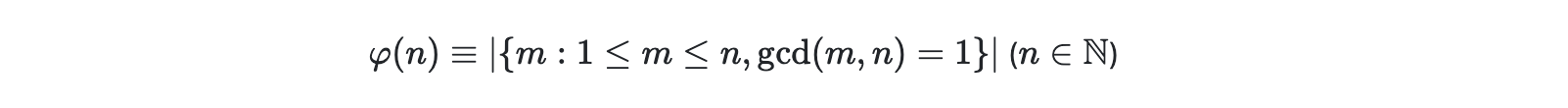
성질

1. 소수 p에 대한 값
   • n이 소수라면, ϕ(p) = p - 1 이다.(소수는 1와 자기 자신을 제외한 모든 숫자와 서로소이다.)
2. 소수의 거듭제곱 p^k에 대한 값
   • n = p^k 라면,

   

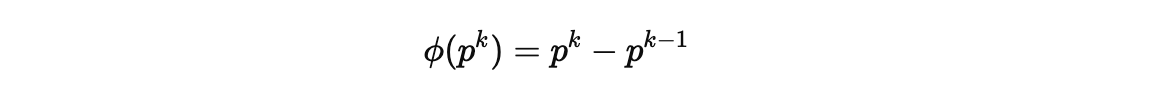
   • p^k보다 작거나 같은 숫자 중 p의 배수는 p^k-1개이고, 이들을 제외한 나머지가 서로소이다.
3. 두 정수의 곱 m*n에 대한 값
   • m과 n이 서로소라면,

   

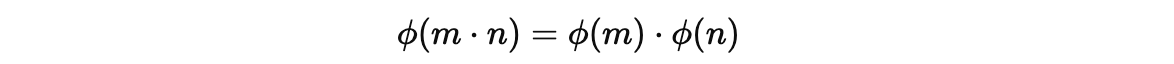
   • 서로소인 두 수는 독립적으로 서로소 조건을 만족한다.

오일러 피 함수의 계산

• 오일러 피 함수를 효율적으로 계산하기 위해 n의 소인수 분해를 활용한다.

• 만약 n의 소인수 분해가 다음과 같다면

  

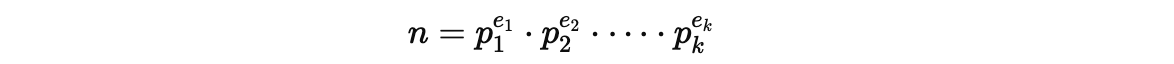
• 오일러 피 함수 공식

  

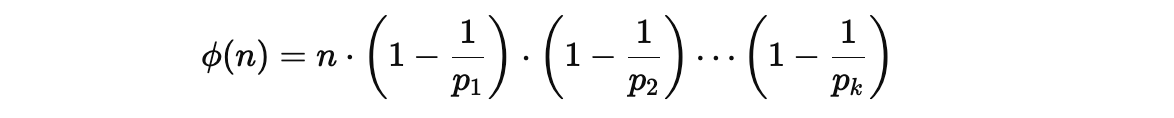
• 예제, n=12라면,
  • 소인수 분해 12 = 2² * 3
  • ϕ(12) = 12 * (1 - 1/2) * (1 - 1/3) = 4
  • ϕ(12) = 4 이므로, 1부터 12까지의 숫자 중 12와 서로소인 숫자는 총 4개이다. (1,5,7,11)

오일러 피 함수 구현하기

오일러 피 함수의 원리

• 동작 방식은 에라토스테네스의 체와 유사하다.

1. 구하고자 하는 오일러 피의 범위만큼 배열을 자기 자신의 인덱스값으로 초기화한다.

2. 2부터 시작해 현재 배열의 값과 인덱스가 같으면(=소수일 때) 현재 선택된 숫자(K)의 배수에 해당하는 수를 배열에 끝까지 탐색하며 P[i] = P[i] - P[i]/K 연산을 수행한다(i는 K의 배수).

3. 배열의 끝까지 (2)를 반복하여 오일러 피 함수를 완성한다.

오일러 피 함수 코드

#include <iostream>
#include <cmath>
using namespace std;

long long eulerPhi(int n){
    int result = n;

    for(int p = 2; p<=sqrt(n); p++){//제곱근까지만 진행
        if(n%p==0){//p가 소인수인지 확인
            result=result-result/p;//결괏값 업데이트
            //해당 소인수 지우기(2^7*11이면 2^7없애고 11만 남김
            while(n%p==0){
                n/=p;
            }
        }
    }

    if(n>1) result -= result / n;..아직 소인수 구성이 남아있는 경우
    //반복문에서 제곱근까지만 탐색했기 때문에 1개의 소인수가 누락되는 케이스

    return result;
}

int main(void){
    int n=12;

    cout<<eulerPhi(12)<<"\n" //출력결과 : 4

    return 0;
}