[알고리즘] 유클리드 호제법(Euclidean-algorithm)

유클리드 호제법

유클리드 호제법은 두 수의 최대 공약수를 구하는 알고리즘이다. 일반적으로 최대 공약수를 구하는 방법은 소인수 분해를 이용한 공통된 소수의 곱으로 표현할 수 있지만 유클리드 호제법은 좀 더 간단한 방법을 제시한다.

핵심 이론

유클리드 호제법을 수행하려면 MOD 연산을 이해하고 있어야한다. MOD 연산이 최대 공약수를 구하는 데 사용하는 핵심 연산이기 때문이다.

• 10 MOD 4 = 2 // 10 % 4 = 2

MOD 연산으로 구현하는 유클리드 호제법

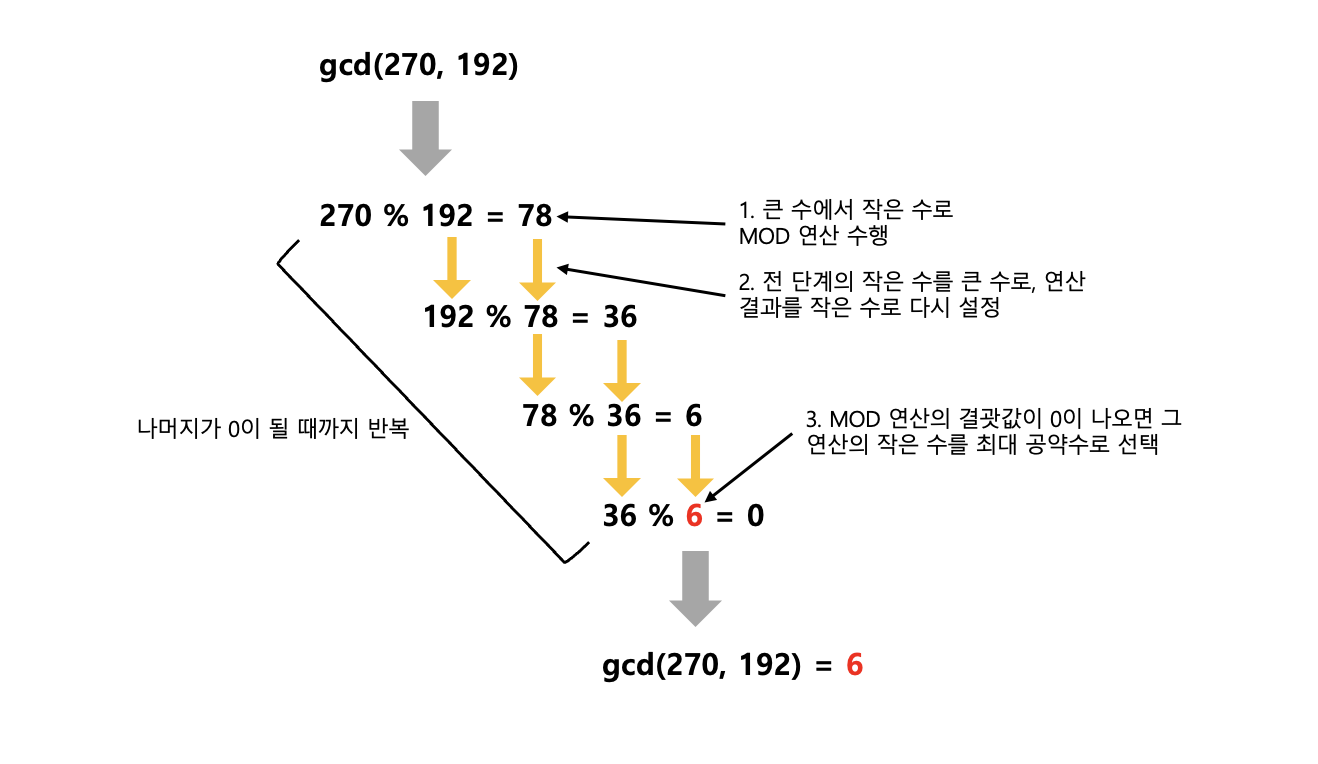
1. 큰 수를 작은 수로 나누는 MOD연산을 수행한다.

2. 앞 단계에서의 작은 수와 MOD 연산 결괏값(나머지)으로 MOD 연산을 수행한다.

3. (2)를 반복하다가 나머지가 0이 되는 순간의 작은 수를 최대 공약수로 선택한다.

유클리드 호제법 원리

최소 공배수 구하기

유클리드 호제법을 사용하여 최소공배수(LCM)을 구하려면, 두 수의 최대공약수(GCD)를 먼저 계산하고 이를 이용해 LCM을 구할 수 있다. 최소 공배수는 아래와 같은 공식을 따른다.

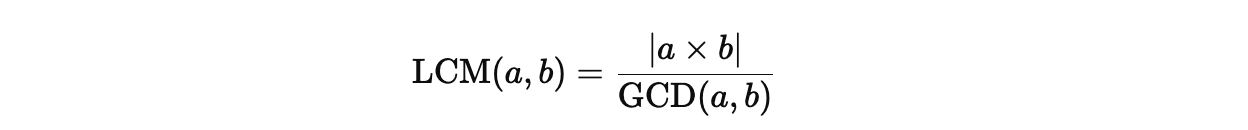
유클리드 호제법 코드 구현

#include <iostream>
#include <cmath>
using namespace std;

//최대 공약수(GCD)를 구하는 함수
int gcd(int a, int b){ 
    if(b==0) return a;

    else return gcd(b, a%b);//재귀 형태로 구현
}

//최소 공배수(LCM)를 구하는 함수
int lcm(int a, int b){ //최대공약수를 이용해 최소공배수를 구하는 공식 그대로 구현
    return (abs(a*b)/gcd(a, b));
}

int main(void){
    int num1 = 18;
    int num2 = 27;

    int result1 = gcd(18, 27);
    int result2 = lcm(18, 28);

    cout<<result1<<" "<<result2<<"\n"//출력 결과 : 9 54

    return 0;
}