[BOJ/백준] 11689번 : GCD(n, k) = 1 (C++)
[BOJ/백준] 11689번 : GCD(n, k) = 1Permalink
문제 해석Permalink
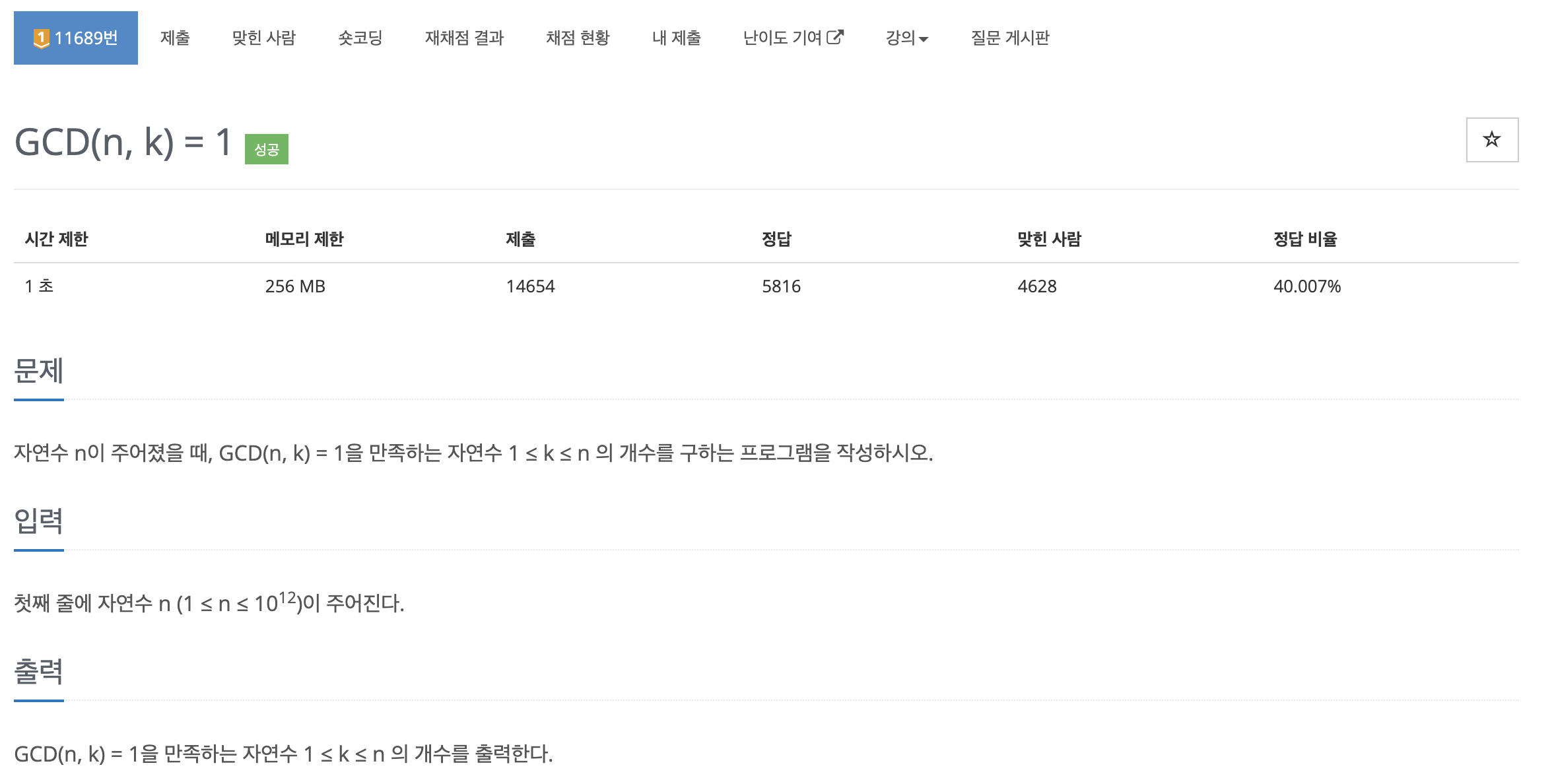
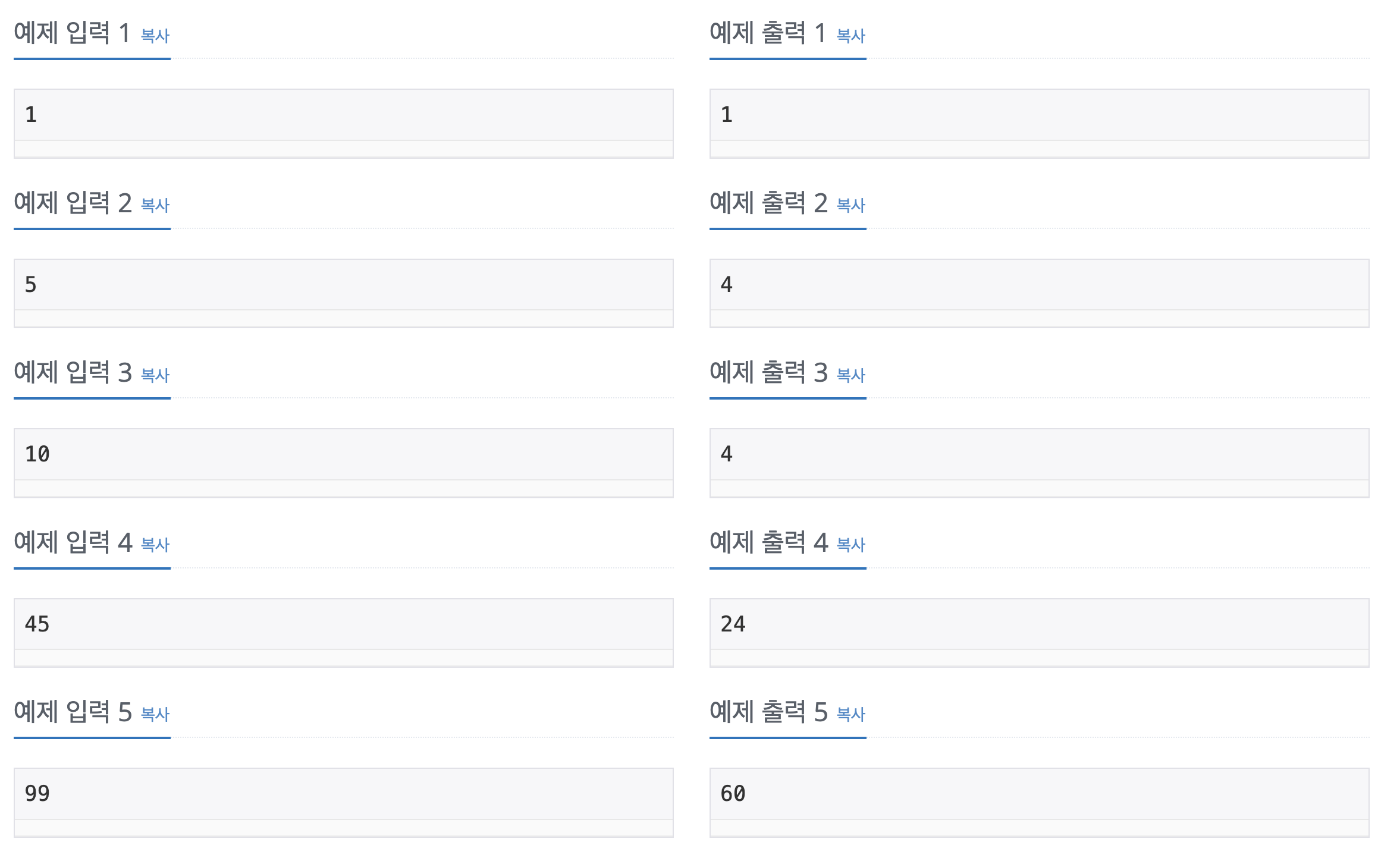
- 문제에서 GCD(n, k) = 1을 만족하는 자연수의 개수는 n과 서로소인 자연수의 개수이다. 즉, 오일러 피 함수의 정의이다.
- 오일러 피 함수
풀이Permalink
- 서로소 개수를 저장하는 변수를 선언한다. 그리고 처음 변수 초기화는 n=서로소 개수 저장 변수로 설정한다.
- n의 제곱근까지 탐색하면서 소인수일 때 p[i]=p[i]-p[i]/k 연산으로 업데이트 해준다.
- 탐색 종료 후 현재 n이 1보다 크면 n이 마지막 소인수라는 의미다. p=p-p/n으로 결과를 마지막으로 업데이트 해준다.
for(2~n의 제곱근까지 반복){
if(현재 값이 소인수){
p=p-p/소인수;
n에서 현재 소인수 내역 제거
}
}
if(n>1) p=p-p/n //n이 마지막 소인수
코드Permalink
#include <iostream>
#include <cmath>
using namespace std;
int main(void){
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
long n;
cin>>n;
long p = n;
for(long p = 2; p<=sqrt(n); p++){
if(n%p==0){
p = p-p/p;
while(n%p==0) n/=p;
}
}
if(n>1){
p = p - p/n;
}
cout<<p<<"\n";
}