[BOJ/백준] 1932번 : 정수 삼각형 (C++)

[BOJ/백준] 1932번 : 정수 삼각형

BOJ 1932

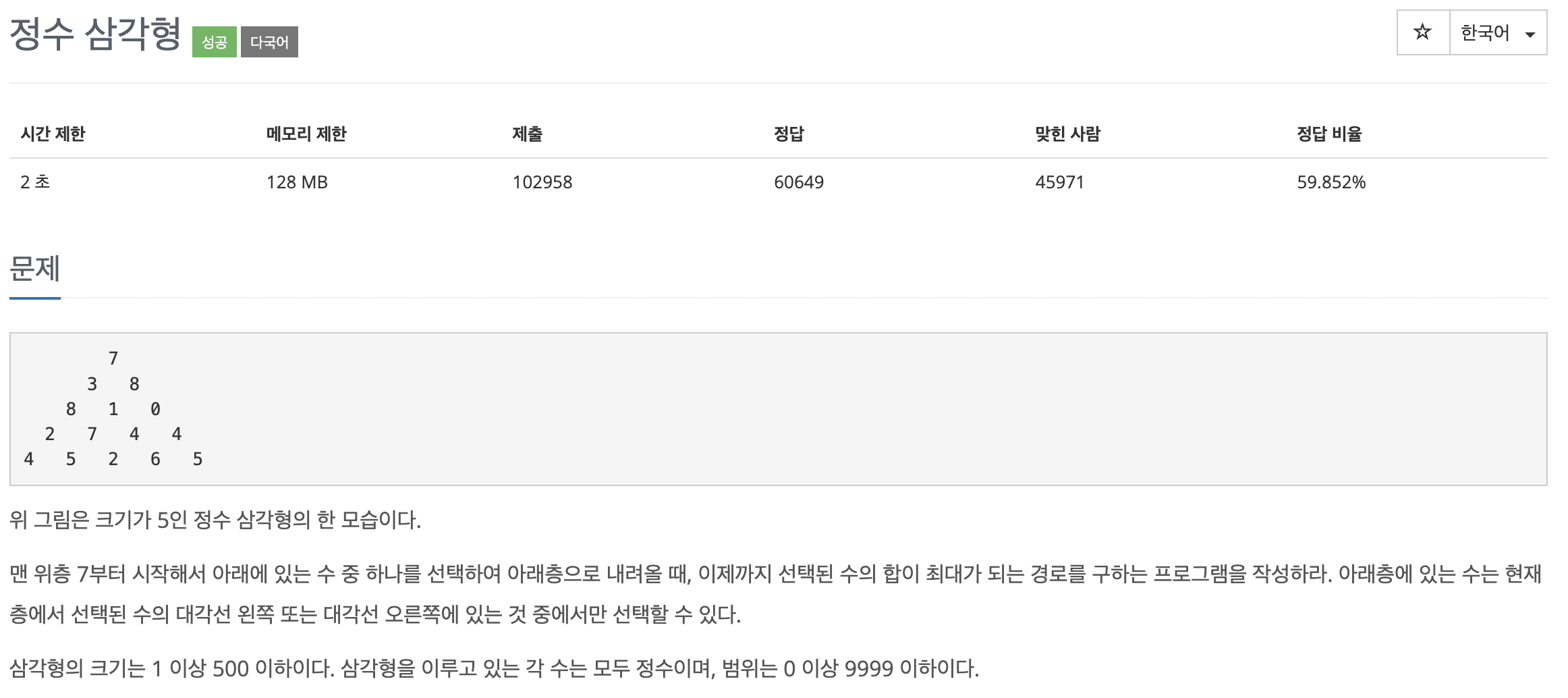
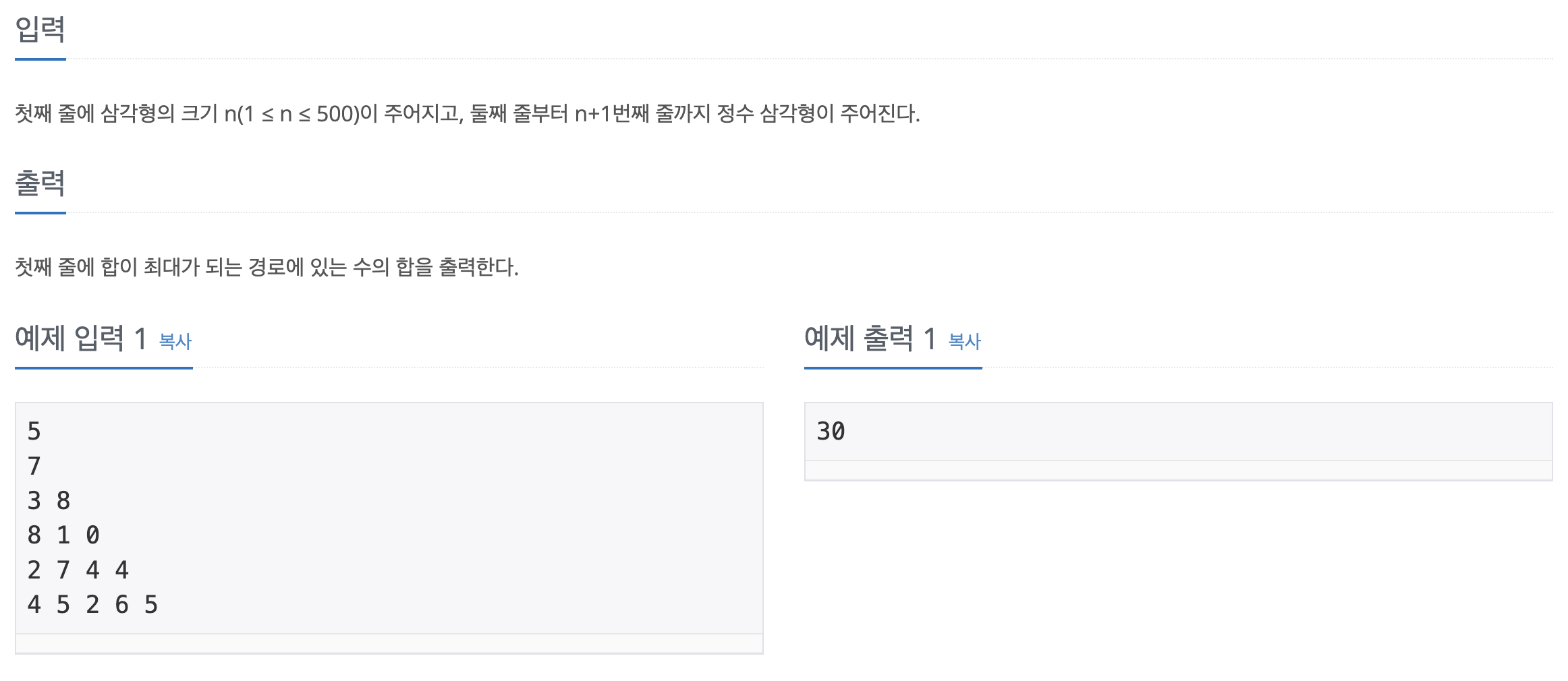
문제 해석

• 주어진 문제에서 “이제까지 선택된 수의 합이 최대가 되는 경로”라는 문장을 보고서는 다이나믹 프로그래밍을 이용해야겠다라는 생각이 들었습니다. 또한 “현재 층에서 선택된 수는 이전 층에서 대각선 왼쪽 또는 대각선 오른쪽의 수 중에서만 선택할 수 있다” 라는 문장을 보고서는 중요한 힌트라고 생각했습니다.

• 문제를 보고 배열은 두 가지를 만들어야겠다고 생각했습니다. 정수 삼각형을 표현할 2차원 배열과 최대 합을 저장할 2차원 배열 이렇게 두 가지입니다.

vector<vector<int> > DP;//최대 합을 저장할 2차원 벡터
vector<vector<int> > A;//정수 삼각형을 표현할 2차원 벡터
...
    int N;
    cin>>N; //삼각형의 크기

    A.resize(N+1, vector<int>(N+1, 0));//인덱스는 1층을 1, 첫번째 노드를 1로 표현하기 위해서 N+1로 설정
    DP.resize(N+1, vector<int>(N+1, 0));

    for(int i=1; i<N+1; i++){
        for(int j=1; j<i+1; j++){//정수 삼각형 초기화
            int s;
            cin>>s;
            A[i][j]=s;
        }
    }

• 여기서 DP 벡터 DP[i][j]는 마지막 층에서 선택되어 더해진 노드가 A[i][j]라는 의미입니다.

풀이

• 저는 현재 층에서 이전 층의 가능한 경로를 탐색하는 방식으로 점화식을 세워봤습니다. 즉, 최종 결과를 기준으로 어떤 경로에서 이 값이 도출되었는지, 이전 항들을 살펴보는 방식입니다.

• 현재 층을 i라고 할 때, i층의 j번째 노드를 선택하였다고 가정하겠습니다. (A[i][j]를 선택)

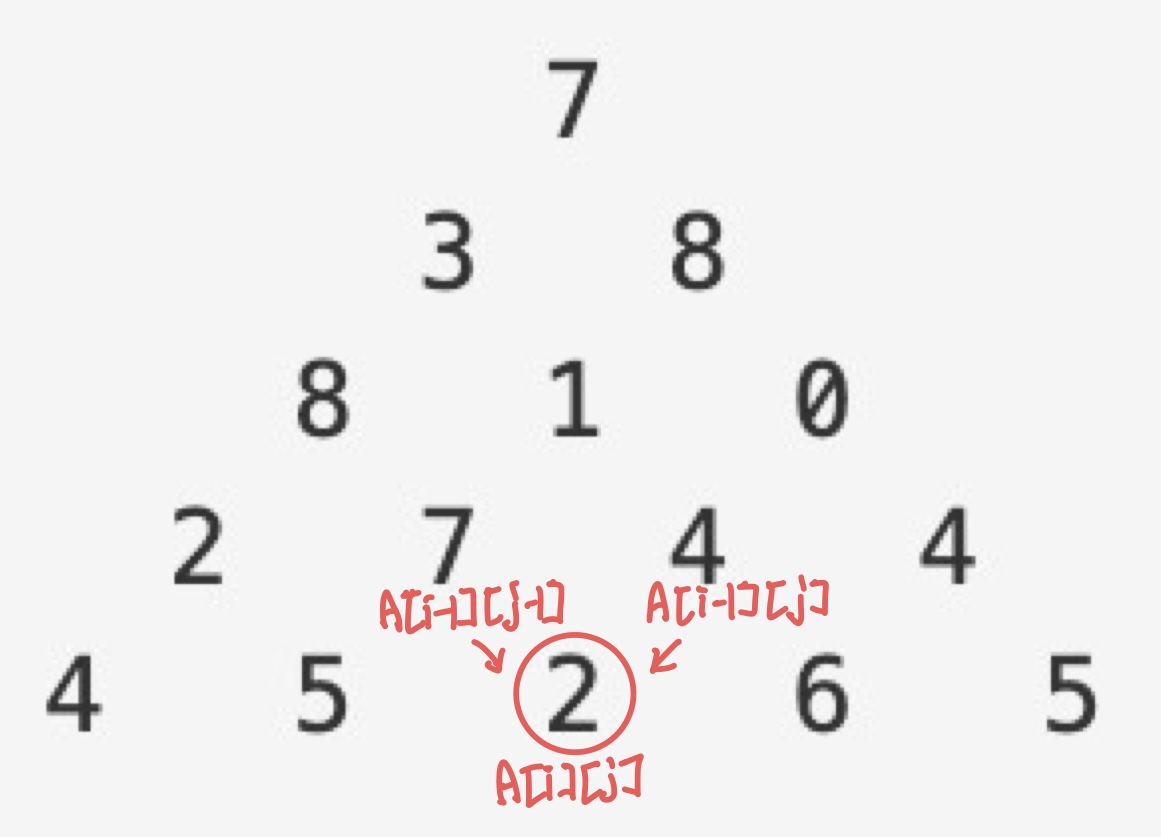
• A[i][j]로 오는 경로 중 i-1번째 층에서 갈 수 있는 위치는 문제 조건에 의해 j-1 과 j 뿐입니다.
• 그러므로 도출되는 점화식은 DP[i][j] = A[i][j] + max(DP[i-1][j-1], DP[i-1][j]) 입니다.

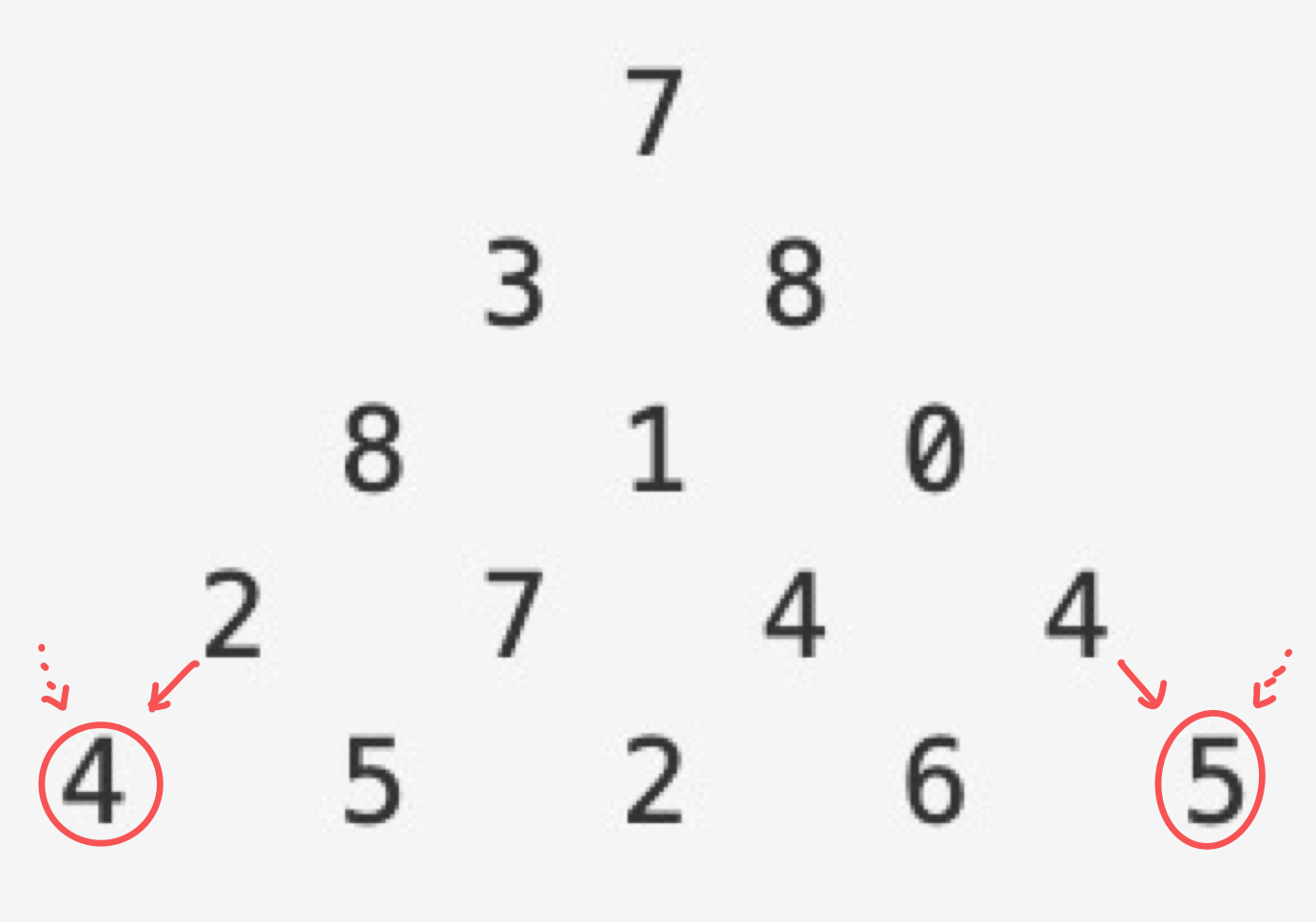
• 하지만 여기서 주의할 점이 있습니다. 각 층의 첫 번째 노드는 왼쪽 위 대각선 노드가 존재하지 않고, 마지막 노드는 오른쪽 위 노드가 존재하지 않습니다. 이 두 경우는 조건문을 이용해 구분을 해주었습니다.

int MaxSum(int n){//파라미터는 삼각형의 크기
    int result=0; //결과를 저장할 변수
    DP[1][1]=A[1][1]; //DP 배열 초기화
    if(n==1) return A[1][1]; //삼각형의 크기가 1이면 A[1][1] 반환

    for(int i=2; i<=n; i++){//2층부터
        for(int j=1; j<i+1; j++){
            if(j==1){//첫번째 노드의 경우 올 수 있는 경로가 A[i-1][j] -> A[i][j]밖에 없음
                DP[i][j]=A[i][j]+DP[i-1][j];
            }
            else if(j==i){//마지막 노드의 경우 A[i-1][j-1] -> A[i][j]밖에 없음
                DP[i][j]=A[i][j]+DP[i-1][j-1];
            }
            else{
                DP[i][j]=A[i][j]+max(DP[i-1][j], DP[i-1][j-1]);
            }
            result = max(result, DP[i][j]);//최댓값으로 result를 업데이트
        }
    }
    return result;
}

코드

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

vector<vector<int> > DP;
vector<vector<int> > A;

int MaxSum(int n){
    int result=0;
    DP[1][1]=A[1][1];
    if(n==1) return A[1][1];

    for(int i=2; i<=n; i++){
        for(int j=1; j<i+1; j++){
            if(j==1){
                DP[i][j]=A[i][j]+DP[i-1][j];
            }
            else if(j==i){
                DP[i][j]=A[i][j]+DP[i-1][j-1];
            }
            else{
                DP[i][j]=A[i][j]+max(DP[i-1][j], DP[i-1][j-1]);
            }
            result = max(result, DP[i][j]);
        }
    }
    return result;
}

int main(void){
    ios::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N; 
    cin>>N; 

    A.resize(N+1, vector<int>(N+1, 0));
    DP.resize(N+1, vector<int>(N+1, 0));

    for(int i=1; i<N+1; i++){
        for(int j=1; j<i+1; j++){
            int s;
            cin>>s;
            A[i][j]=s;
        }
    }

    int result=0;

    result = MaxSum(N);

    cout<<result;
    return 0;
}