[컴퓨터 구조] 컴퓨터 산술 연산 Integer 곱셈, 나눗셈

곱셈 (Multiplication)

정수 곱셈의 기본 원리

컴퓨터에서의 곱셈은 우리가 수학 시간에 배운 긴 곱셈(long multiplication)과 매우 유사한 방식으로 시작된다.

        1000    (8)  multiplicand
      x 1001    (9)  multiplier
     --------
        1000    <- 1 * 1000 (LSB = 1)
       0000     <- 0 * 1000
      0000      <- 0 * 1000
     1000       <- 1 * 1000
     -------- 
     1001000    <- 총합( 8 * 9 = 72 ) Product

• 각각의 비트를 확인하며 0이면 생략, 1이면 multiplicand를 왼쪽으로 이동한 값을 더함(left shift)
• 최종 결과의 길이 = multiplicand와 multiplier 비트 수의 합

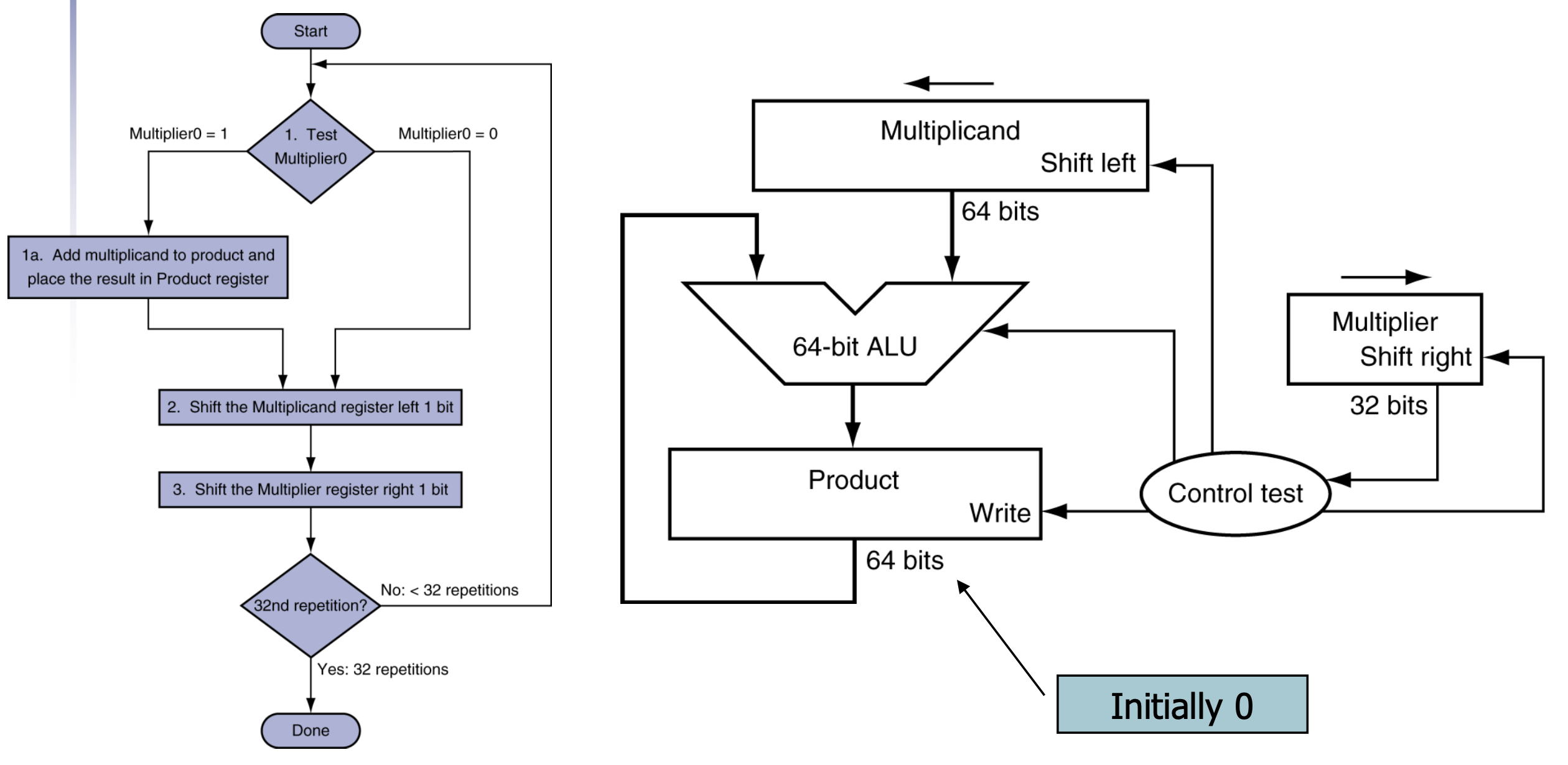
곱셈 연산의 하드웨어 구조

컴퓨터는 인간이 계산하듯 곱셈을 직관적으로 처리하지 않는다. 위에 방식 처럼, 단순한 덧셈과 시프트 연산만을 반복하여 곱셈을 구현한다. 이 방식은 하드웨어로 쉽게 자동화할 수 있으며, Shift-and-Add 곱셈기라는 구조로 널리 사용된다.

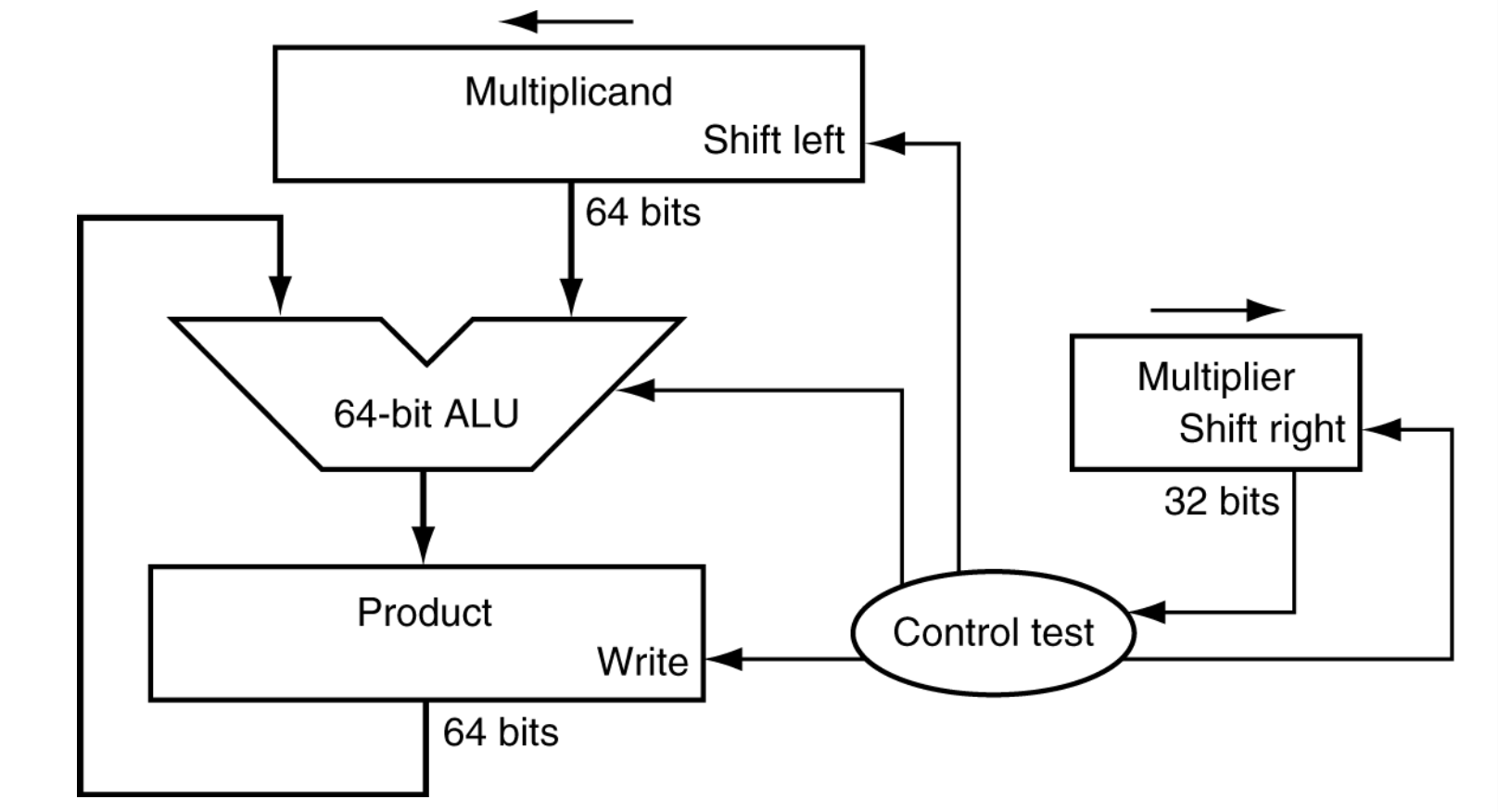
• ALU(산술논리연산장치) : 연산 수행, Control Test가 덧셈 연산 또는 뺄셈 연산에 대한 시그널을 보내면, 그에 맞는 연산을 수행한다.
• Multiplicand Register : 피승수 저장 및 시프트 처리
• Multiplier Register : 승수 저장 및 시프트 처리
• Product Register : 연산 결과 누적 저장, 초기값은 0이며 조건에 따라 ALU 결과가 기록된다.
• Control Unit(제어 유닛) : 연산 흐름 제어 및 Write 신호 결정. Multiplier의 LSB를 확인하고 ALU 연산 여부와 Write 신호를 결정. 시프트 타이밍도 제어한다.
  • LSB = 1 : Write 신호 활성화
  • LSB = 0 : Write 없으므로 Product 갱신이 안된다.

위 구조는 Shift-and-Add 곱셈기로, 다음의 순서로 작동한다.

1. Multiplier의 LSB(최하위 비트)를 검사
2. 1이면 Product에 Multiplicand를 더함
3. Multiplicand는 왼쪽으로 시프트
4. Multiplier는 오른쪽으로 시프트
5. 위 과정을 비트 수만큼 반복

• 단계별 예시 : 8 x 9

        1000    (8)  multiplicand
      x 1001    (9)  multiplier
     --------
        1000    <- 1 * 1000 (LSB = 1)
       0000     <- 0 * 1000
      0000      <- 0 * 1000
     1000       <- 1 * 1000
     -------- 
     1001000    <- 총합( 8 * 9 = 72 ) Product

• Product = 0 초기화

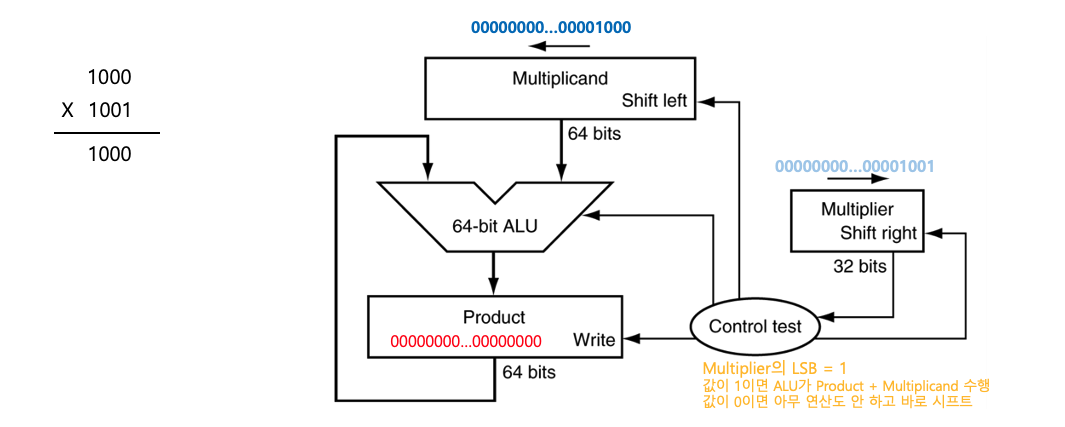
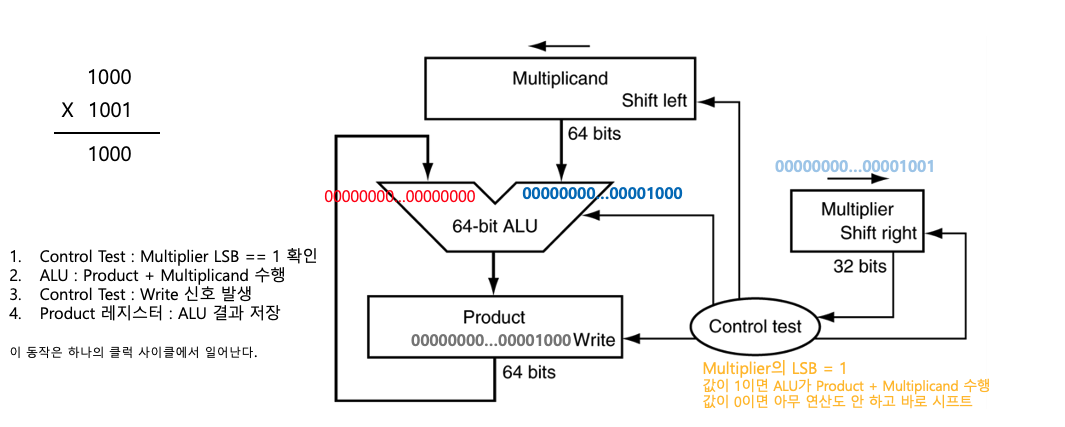
• Step1

  • Multiplier LSB = 1
  • ALU: 0 + 8 = 8
  • Product ← 8
  • Multiplicand «= 1 → 16, Multiplier »= 1 → 4
  • Write 수행

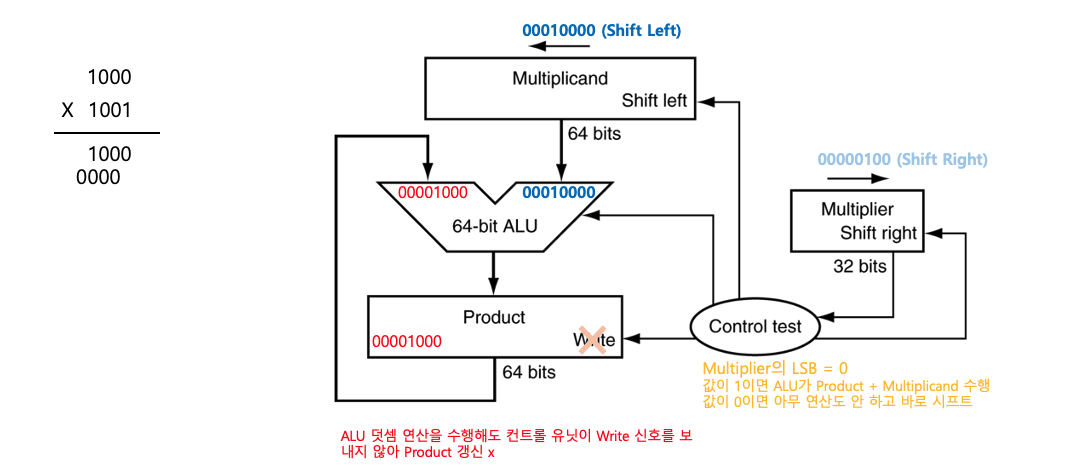
• Step2
  • Multiplier LSB = 0
  • ALU: 0 + 8
  • Product ← 8
  • Write 수행 x(Write 수행을하지 않으면, 연산을 수행하지 않은 것과 동일함)

• Step3
  • Multiplier LSB = 0
  • ALU: 0 + 8
  • Product ← 8
  • Write 수행 x

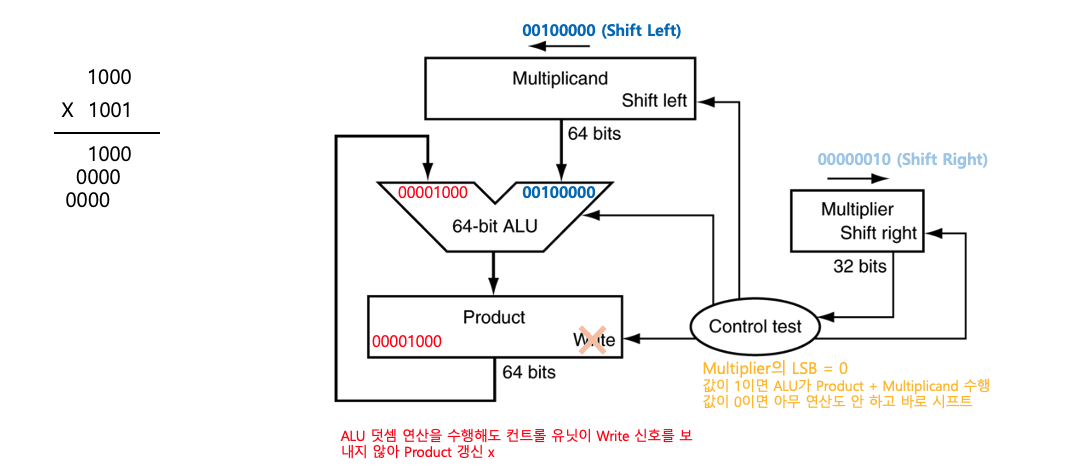
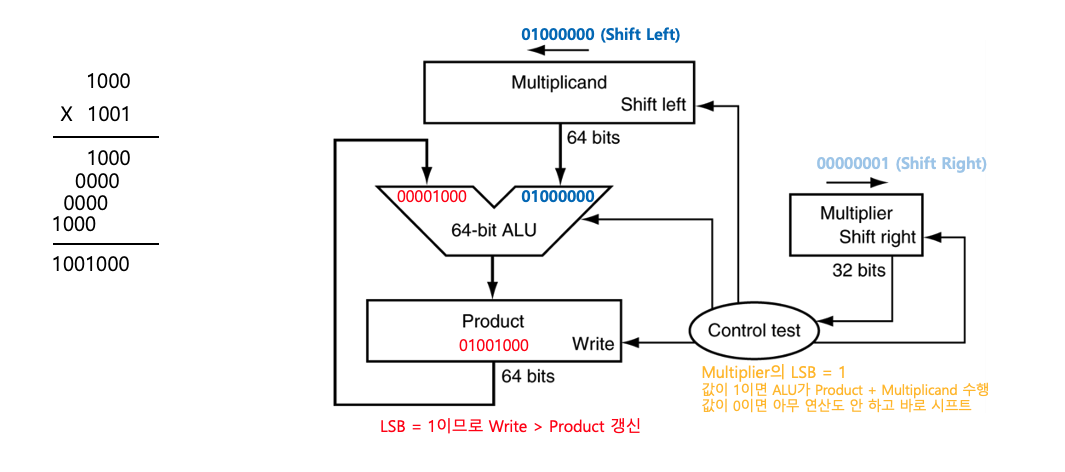
• Step4
  • Multiplier LSB = 1
  • ALU: 연산 수행 8 + 64 = 72
  • Product ← 72
  • Write 수행

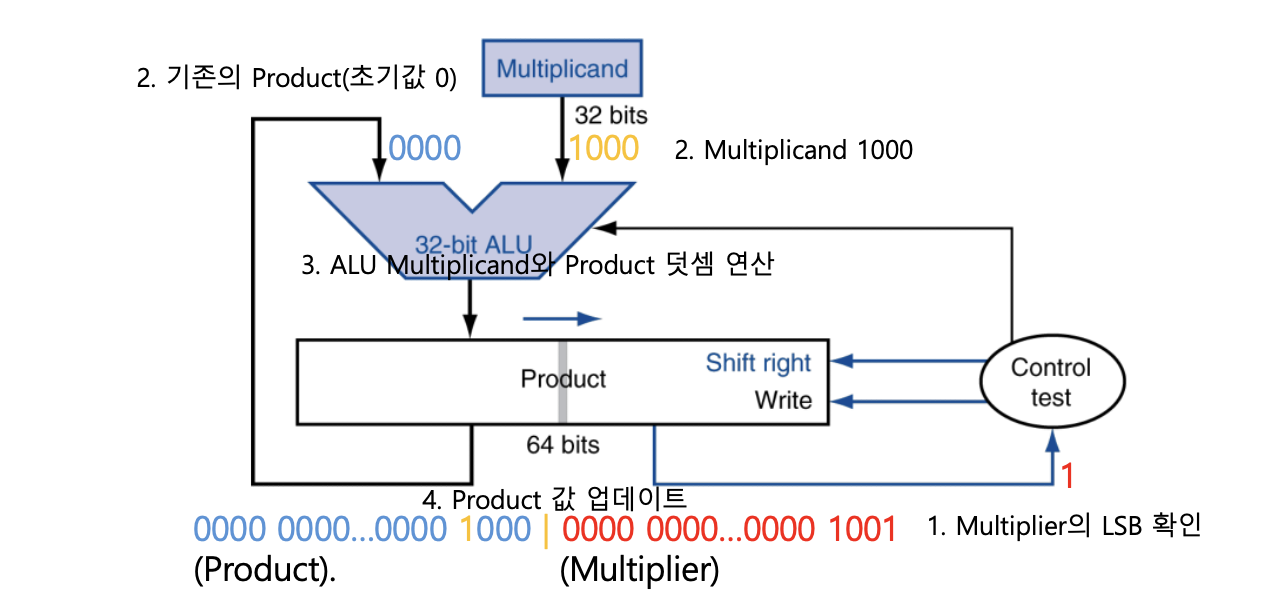
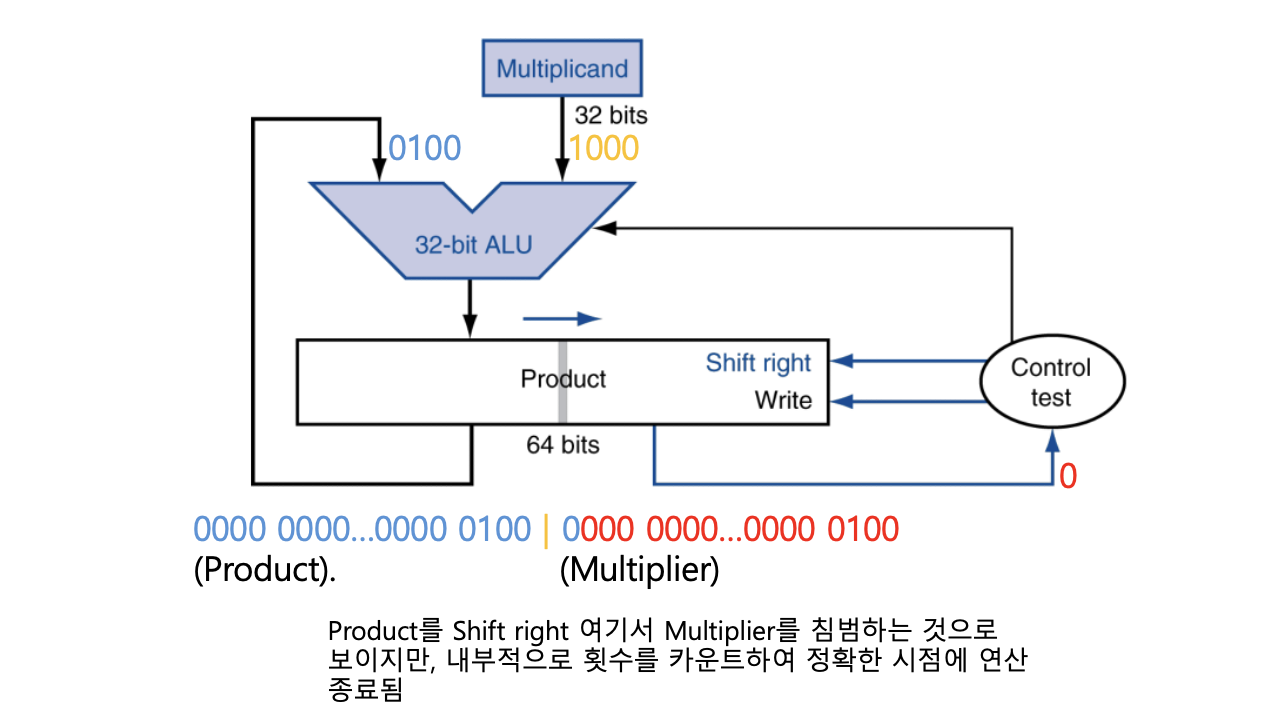
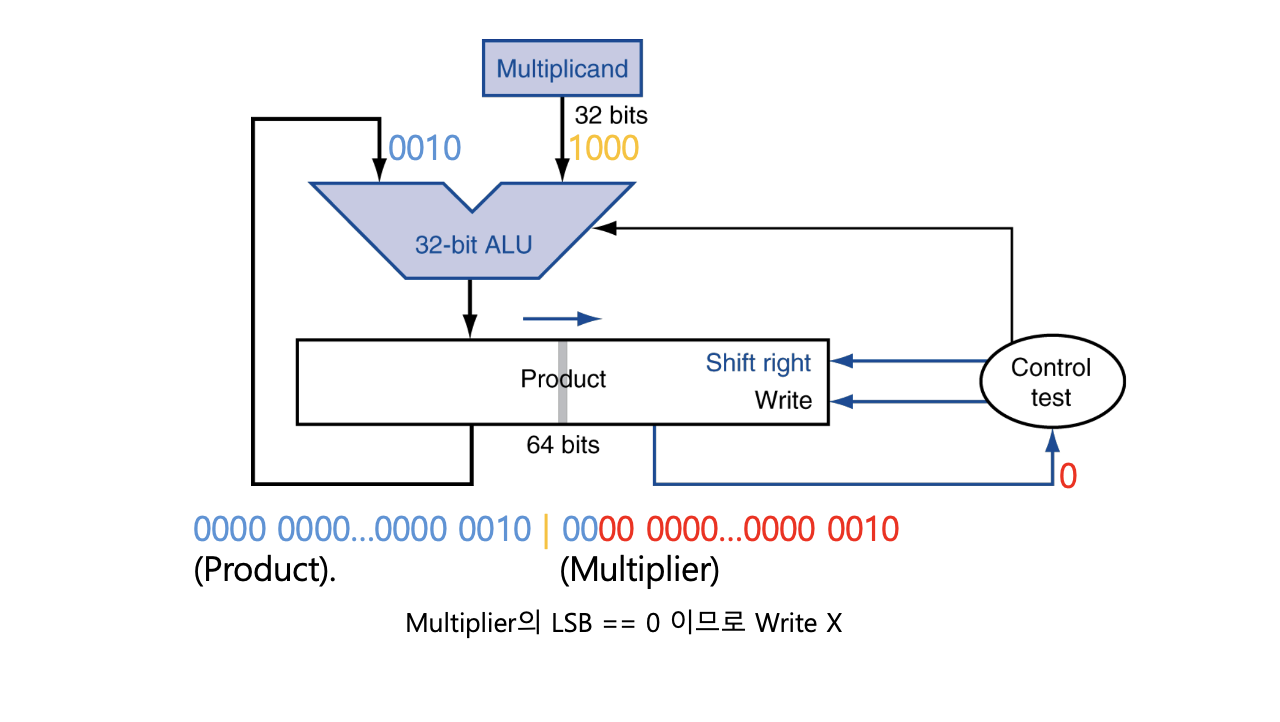
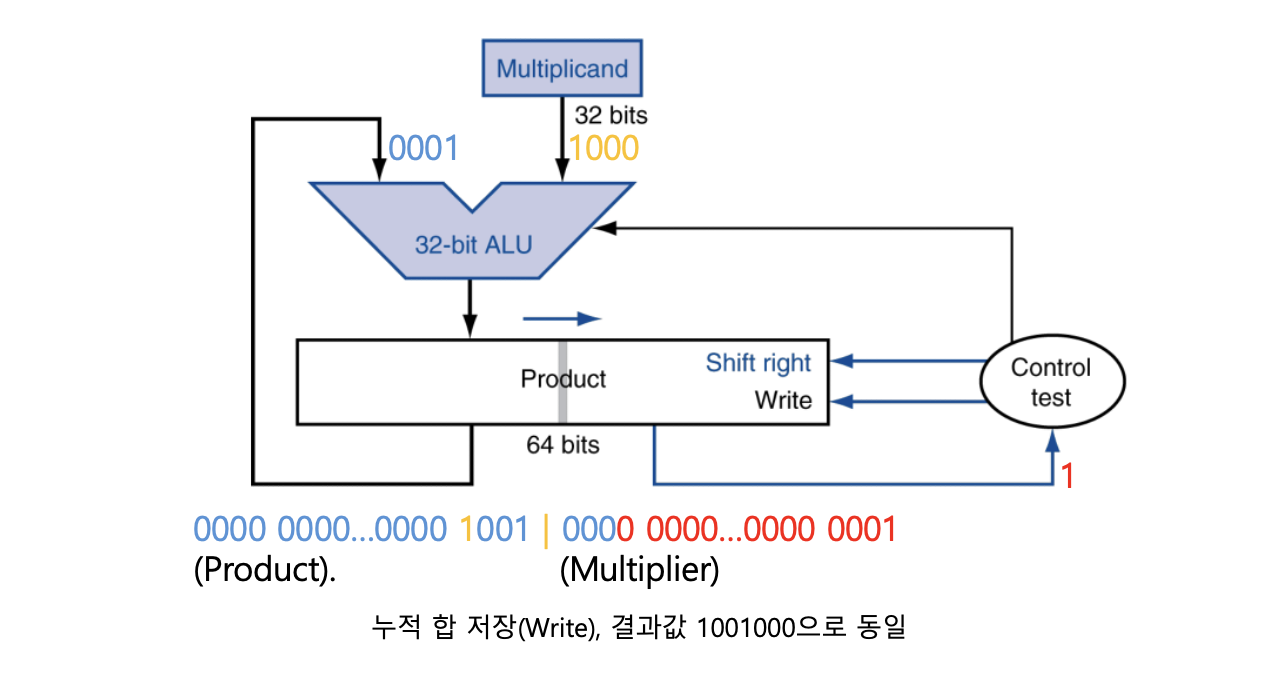
Optimized Multiplier

Optimized Multiplier는 MIPS와 같은 32비트 시스템에서 곱셈을 수행할 때, 기존의 곱셈기 구조를 간소화하면서도 정확한 결과를 만들 수 있도록 설계된 하드웨어 구조이다.

기존 곱셈기는 Multiplicand를 shift-left하고, Multiplier는 별도 레지스터에 유지했지만, Optimized Multiplier는 Product 레지스터 하나로 둘을 함께 처리하며 효율을 높인다.

구조

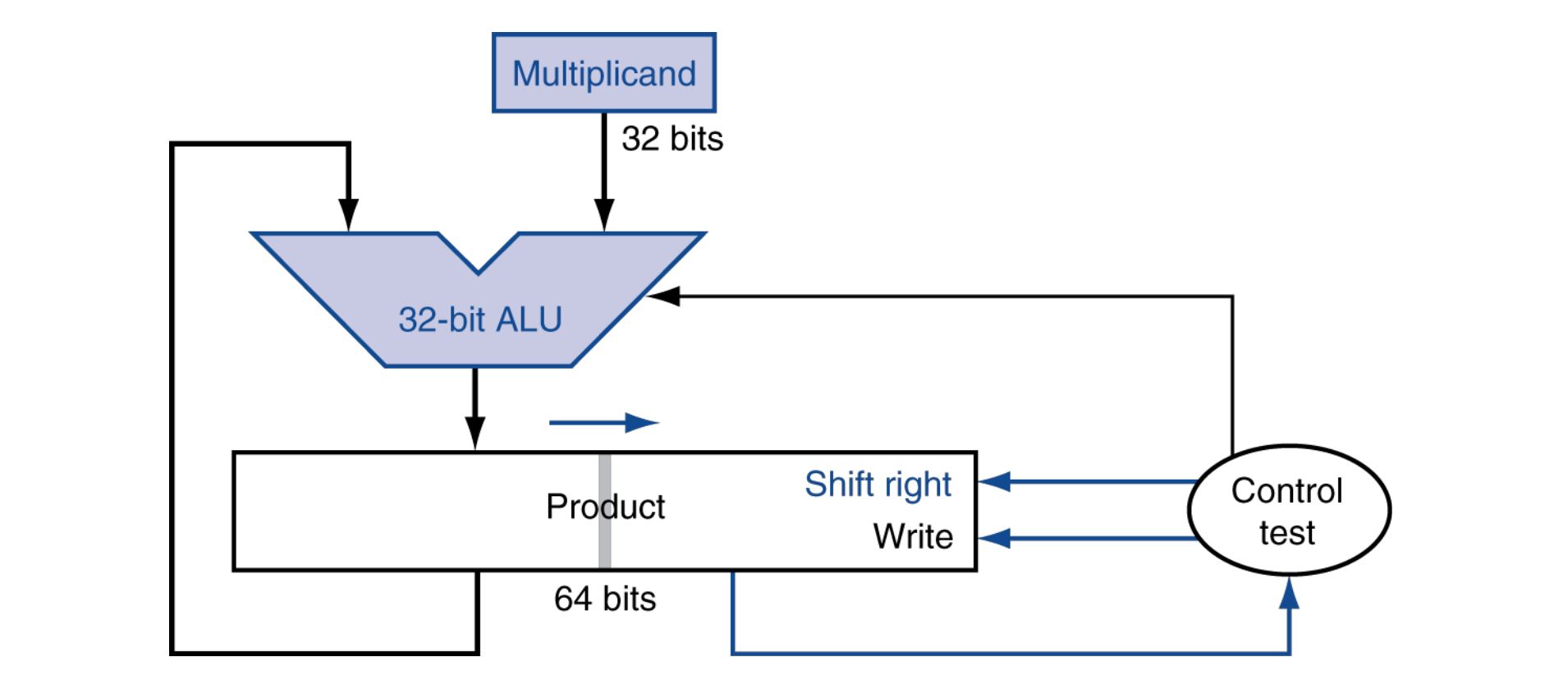
Product 레지스터: 64비트
[ 63 ................................ 32 | 31 ....................... 0 ]
← 결과 누적 공간 (상위)              | ← 초기 Multiplier (하위)

• Multiplicand는 별도 고정 레지스터에 있다.
• Product의 하위 32비트에는 Multiplier가 미리 채워져 있다.
• 곱셈 결과는 Product 전체에 64비트로 누적됨

동작 흐름

Faster Multiplier

Faster Multiplier는 시간 지연을 줄이기 위해, 곱셈 과정을 병렬화한 구조이다. 각 비트마다 곱셈 결과(Partial Product)를 만들어 놓고, 이 partial product들을 동시에 더하는 구조이다. 더 이상 한 사이클마다 Shift하면서 기다리지 않게된다.

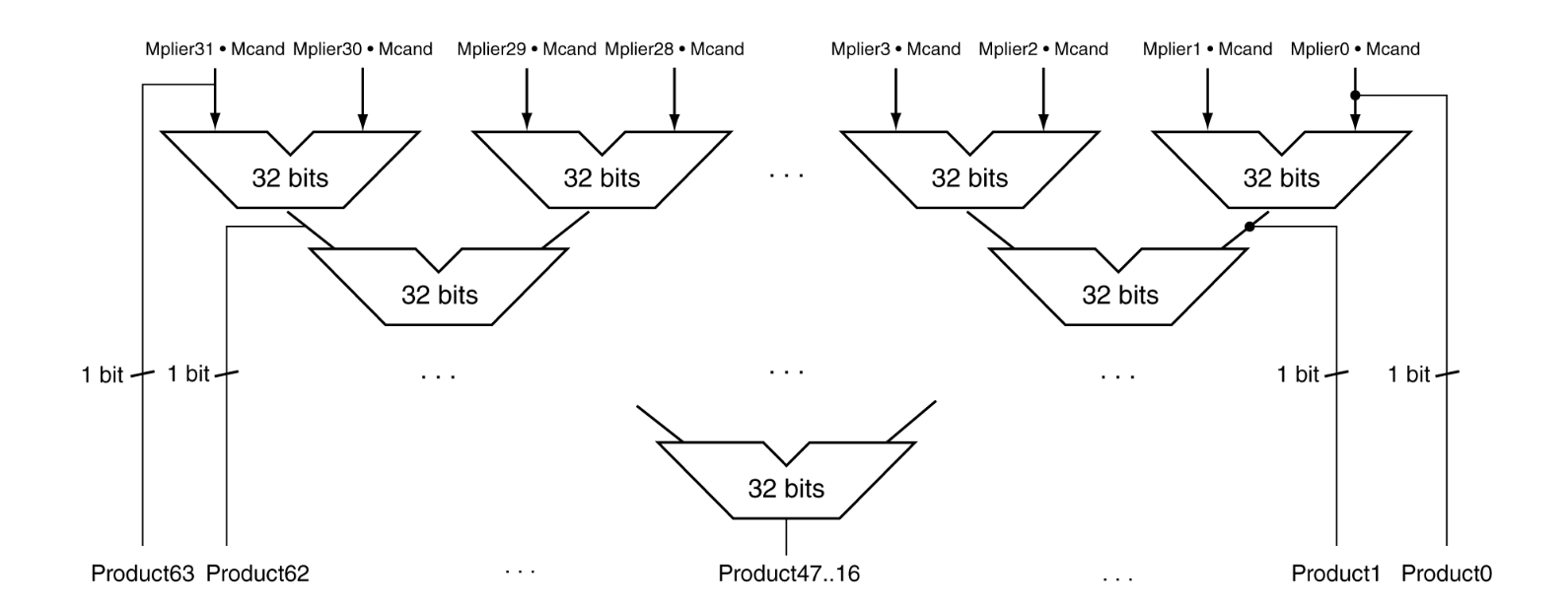
✅부분곱 생성 단계: Mplier[i] * Mcand : 각 비트 Mplier[i]에 대해 32비트 multiplicand와 AND 연산 수행 -> 32비트 Partial Product 생성

✅부분곱 정렬 및 더하기 : 생성된 부분곱은 각각 2ⁱ 자리수에 해당되므로, 실제 곱처럼 각 비트를 오른쪽으로 i 비트만큼 shift한 효과가 필요하다. 위 그림에서는 그런 시프트된 부분곱을 계단식으로 아래로 정렬해서 시각적으로 표현했다.

✅덧셈 단계 : 병렬 32비트 adder 사용 : 각 단계에서 두 개의 32비트 값을 한 번에 더한다. 이를 트리구조로 계속해서 합쳐 나간다.

• 즉, Mplier의 각 비트와 Mcand를 곱한 결과를 한 번에 만들고, 그걸 빠르게 더해가며 결과를 만들어내는 구조이다.
• 마지막에 더해진 결과가 바로 64비트 Product, 즉 Product[63:0]에 저장된다.

나눗셈 (Division)

나눗셈 연산 : Restoring Division Algorithm

Restoring Division Algorithm(복원 나눗셈)은 CPU가 정수 나눗셈을 수행하는 대표적인 방법 중 하나로, 쉬프트 + 빼기 + 조건 판단 + 복원(add back)의 과정을 반복하면서 몫(Quotient)과 나머지(Remainder)를 계산하는 방식이다.

정수 나눗셈의 기본 원리

컴퓨터에서의 나눗셈은 우리가 수학 시간에 배운 긴 나눗셈(long division) 방식과 유사하게 작동한다. 다만, 컴퓨터는 뺄셈과 시프트만으로 몫과 나머지를 계산하며, 이 과정은 정해진 패턴에 따라 자동화된다.

         1001010  (74)  dividend
      ÷     1000 (8)   divisor
    ------------------------
         1번: 1001 - 1000 = 0001 → 몫 1, 나머지 1
         2번: 0010 - 1000 = 음수 → 복원, 몫 0
         3번: 1010 - 1000 = 0010 → 몫 1
         ...
    ------------------------
         quotient = 1001 (9), remainder = 10 (2)

• dividend 상위 비트부터 시작하여 divisor를 뺀다.
• 결과가 0이상이면 몫 자리에 1, 음수면 복원(add back)하고 몫에 0
• 이 과정을 반복하며 최종 몫과 나머지를 계산한다.

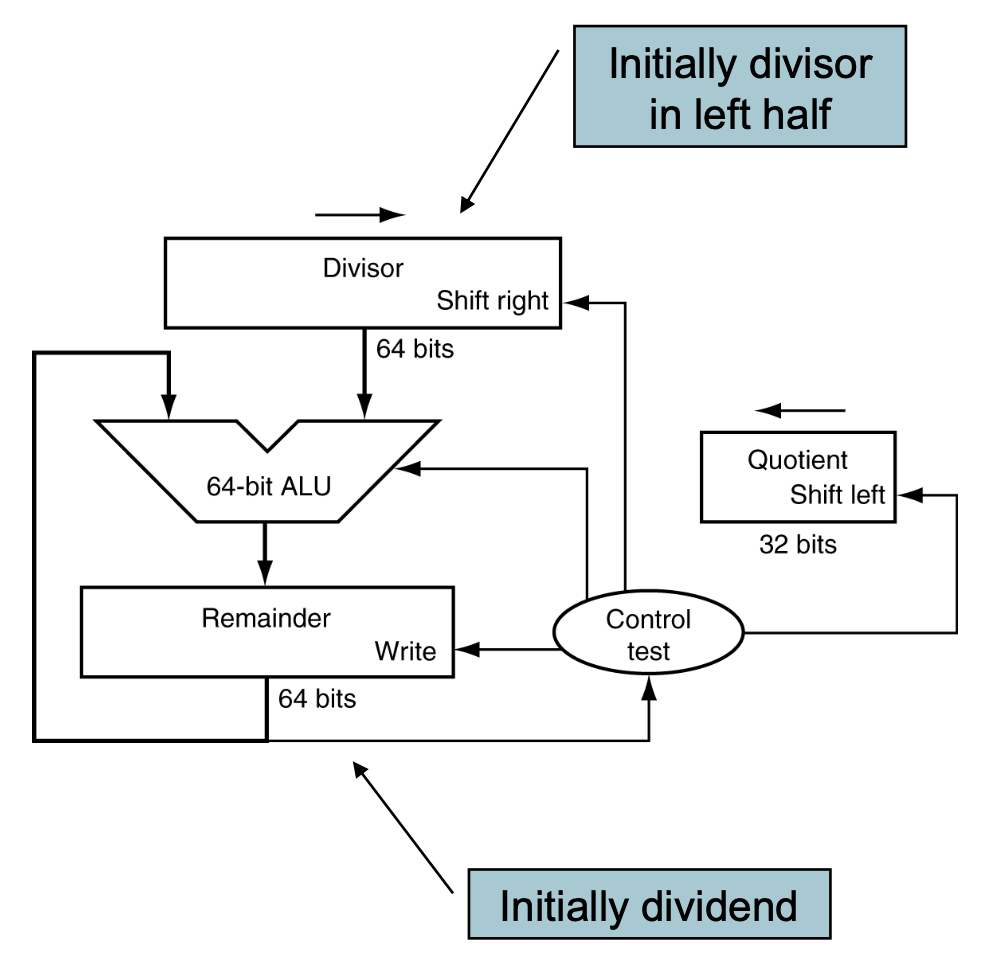
나눗셈 연산의 하드웨어 구조

컴퓨터에서 정수 나눗셈을 수행하기 위한 최로는 주로 Restoring Division(복원 나눗셈) 알고리즘을 구현한 구조를 갖는다. 이 구조는 뺄셈 -> 조건 확인 -> 복원 여부 판단 -> 시프트를 반복하는 방식으로 몫과 나머지를 계산한다.

• ALU(산술논리연산장치) : 뺄셈 및 복원(add back) 연산을 수행한다.
• Divisor Register : 나누는 수를 저장, Remainder와의 연산 시 ALU에 입력된다.
• Remainder Register : 나머지를 저장하며, 처음에는 dividend의 상위 비트가 들어간다.
• Quotient Register : 연산 결과인 몫을 저장. 시프트되며 새로운 비트를 왼쪽에서 채운다.
• Control Unit(제어 유닛) : Reamainder가 음수인지 확인하고, ALU 연산 방향(빼기 or 복원), Quotient 비트 결정, 시프트 제어를 수행한다.
  • Remainder ≥ 0 : Quotient에 1 저장
  • Remainder < 0 : 복원 후 Quitient에 0 저장

Resotring Division의 순서

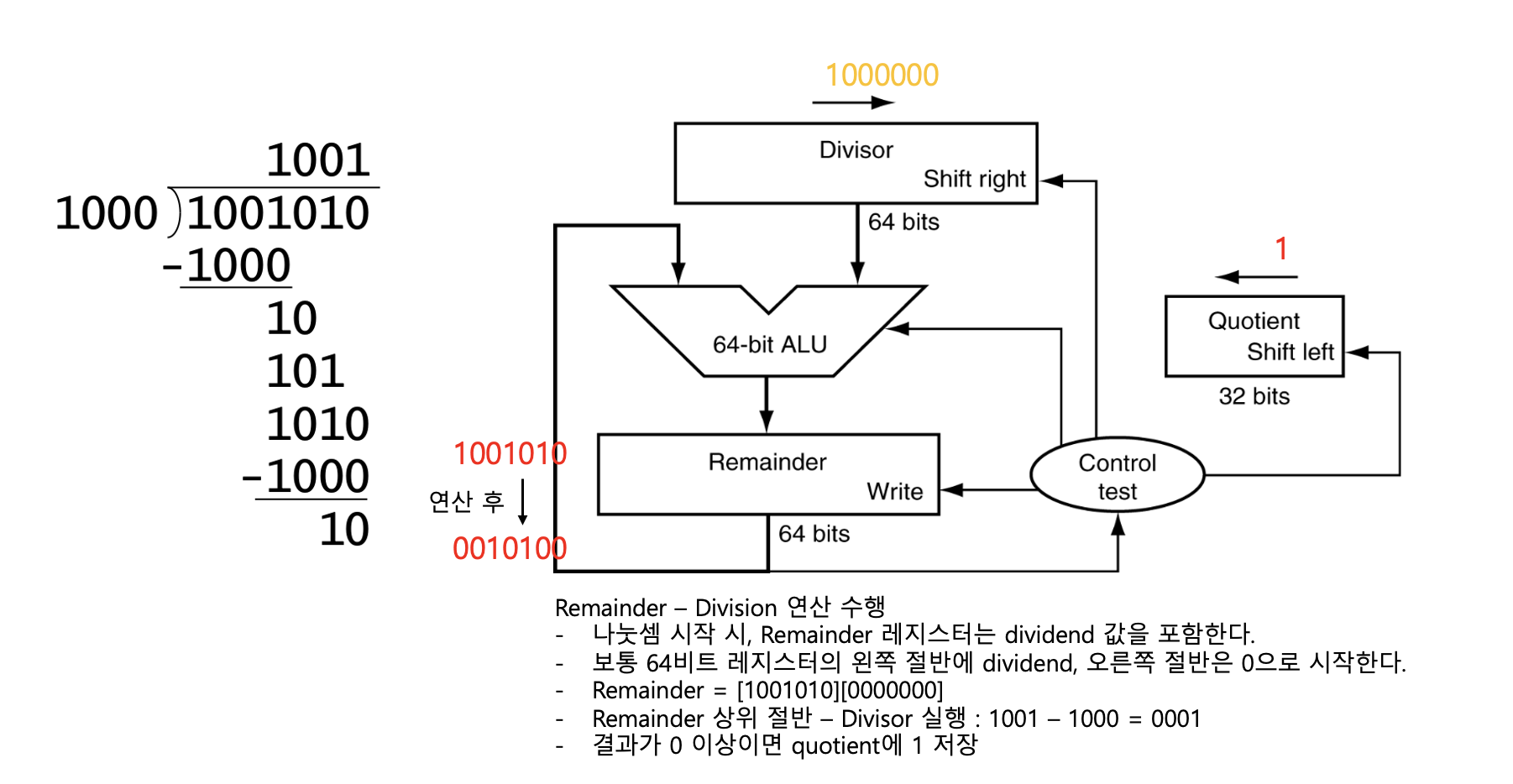
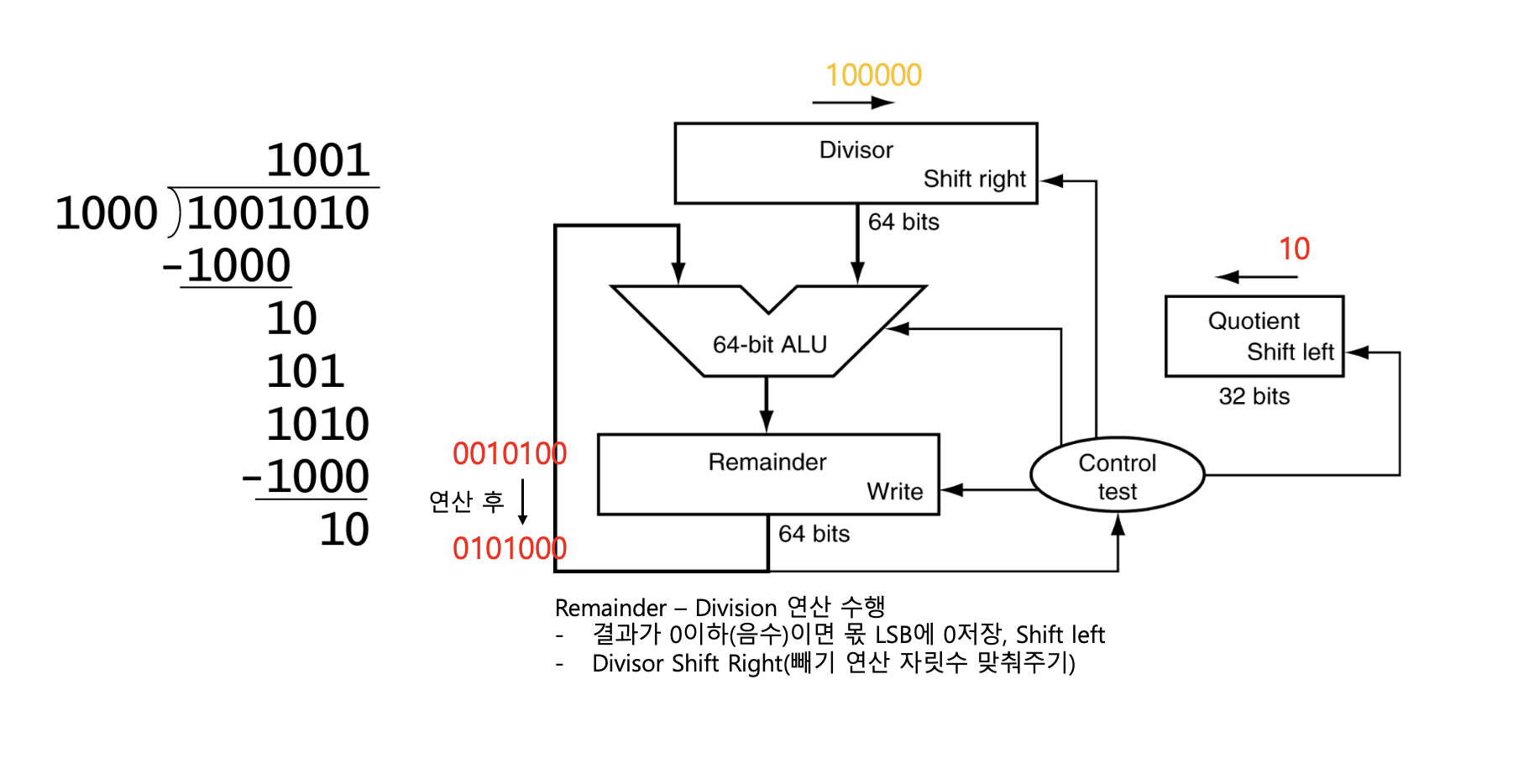
1. Divisor를 Remainder에서 뺌
2. Remainder가 0이상이면 몫의 LSB에 1저장
3. Remainder가 음수이면 복원(add back), 몫의 LSB에 0 저장
4. Quotient 레지스터를 왼쪽으로 시프트
5. Remainder도 시프트하거나, Divisor를 오른쪽으로 시프트
6. 위 과정을 비트 수(예: 32회)만큼 반복

Optimized Divider

Optimized Divider는 Remainder 레지스터 하나만으로 나머지와 몫을 동시에 관리하며 나눗셈을 수행하는 구조이다. 일반 구조에서는 Remainder와 Quotient를 따로 관리하며, 이 구조에서는 64비트 Remainder 안에 Quotient 비트를 누적시켜 저장한다.

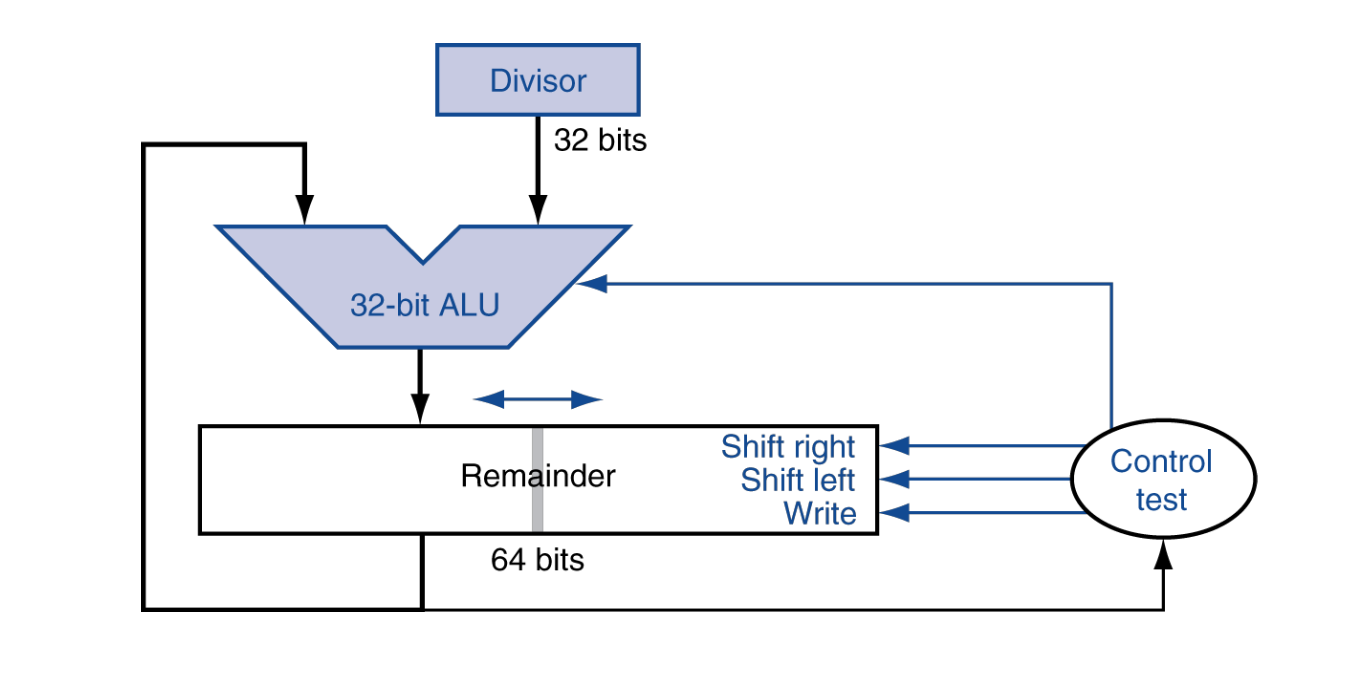
최적화 부분

1. Quotient 레지스터 제거 : Quotient를 따로 저장하지 않고, Remainder의 하위 비트에 몫을 저장
2. 64비트 Remainder 통합 : 상위 비트는 나머지 계산용, 하위 비트는 quotient 누적용
3. ALU 연산 범위 축소 : ALU는 32비트만 사용(상위 비트 연산만 필요). 전체 64비트를 연산하는 비용 절감

Faster Division

한계: 곱셈기처럼 병렬 회로(parallel hardware)를 그대로 사용할 수는 없다. 곱셈기(Faster Multiplier)는 Partial Product를 미리 만들어 병렬로 더할 수 있었지만, 나눗셈은 연산이 직전 결과(특히 remainder의 부호)에 따라 달라지기 때문에 병렬로 미리 연산을 진행할 수 없다.

Substarction이 remainder의 부호(sign)에 따라 조건부로 결정된다. 매 step마다 remainder - divisor 결과가 양수냐 음수냐에 따라 quotient 비트가 달라지며, 다음 연산 경로가 바뀐다. 이 때문에 완전한 병렬화가 어렵다.