[컴퓨터 구조] 부동 소수점 (Floating Point)

Floating Point - 부동 소수점

컴퓨터는 정수뿐만 아니라 실수(real number)도 표현할 수 있어야 한다. 특히 과학 계산, 그래픽스, 신호 처리와 같은 분야에서는 아주 크거나 아주 작은 수를 정확하게 표현하는 것이 중요하다.

이러한 실수 표현은 우리가 수학에서 사용하는 과학적 표기법(scientific notation)과 유사한 형태로 처리된다.

예를 들어, 아래와 같은 수를 생각해 보자.

-2.34 × 10⁵⁶  
+0.002 × 10⁻⁴  
+987.02 × 10⁹

컴퓨터는 이를 이진 부동소수점 표기법으로 변환하여 다룬다. 이진에서는 다음과 같은 형태로 표현된다.

±1.xxxxx × 2^yyyy

이때, 1.xxxxx는 정규화된(significand or mantissa) 부분, 2^yyyy는 지수(exponent) 부분을 나타낸다. 이 구조는 float, double과 같은 자료형으로 구현된다.

IEEE 754 부동소수점 표준

과거에는 컴퓨텉마다 실수를 표현하는 방식이 달라 프로그램의 이식성(portability)에 문제가 있었다. 이 문제를 해결하기 위해, IEEE는 1985년에 IEEE 754 표준을 정의했고, 지금은 거의 모든 시스템에서 이를 따른다.

IEEE 754는 크게 두 가지 표현 방식을 제공한다.

• 단정밀도(Single Precision) : 32비트
• 배정밀도(Double Precision) : 64비트

IEEE 부동소수점 표현 형식

부동소수점 숫자는 다음과 같은 구조로 구성된다.

• 부호 비트(S) : 1비트 (0은 양수, 1은 음수)
• 지수(E) : Bias 방식으로 저장
  • 단정도(Single Precision) : bias = 127
  • 배정밀도(Double Precision) : bias = 1023
• 가수(Fraction F) : 소수 부분(정규화되어 항상 1.xxx 형태, 그래서 1.은 저장하지 않음 -> hidden bit)

부동소수점 표현 예제

실수 -0.75를 IEEE 754 단정도 형식으로 표현

1. 실수를 이진수로 바꾸기

–0.75 = –(0.5 + 0.25) = –(2⁻¹ + 2⁻²) = –0.112₂

1. 정규화

–0.75 = –1.1 × 2⁻¹

1. 비트 필드 계산
   • 부호 비트(S) : 1(음수는 1, 양수는 0)
   • 지수(E) : 126(01111110), 실제 지수는 -1, Bias = 127 -> E = -1 + 127 = 126
   • 가수(Fraction) : 10000000000000000000000 정규화된 값 1.1 -> 소수 부분 1 저장
2. 최종 비트 조합(32비트)

S EEEEEEEE FFFFFFFFFFFFFFFFFFFFFFF
1 01111110 10000000000000000000000

단정밀도 Single-Precision Range

표현 범위 및 정밀도

• 최소값 : ±1.0 × 2⁻¹²⁶ ≈ ±1.2 × 10⁻³⁸
• 최대값 : ±2.0 × 2¹²⁷ ≈ ±3.4 × 10³⁸
• 정밀도 : 약 6자리(10진수)

배정밀도 Double-Precision Range

표현 범위 및 정밀도

• 최소값 : ±1.0 × 2⁻¹⁰²² ≈ ±2.2 × 10⁻³⁰⁸
• 최대값 : ±2.0 × 2¹⁰²³ ≈ ±1.8 × 10³⁰⁸
• 정밀도 : 약 16자리(10진수)

부동소수점 연산

부동소수점 덧셈/곱셈은 정수 연산보다 복잡하다. 덧셈의 예를 들어보면, 다음과 같은 과정을 따른다.

부동소수점 덧셈 단계

1. 지수 정렬 : 지수가 작은 쪽의 가수를 오른쪽으로 shift
2. 가수 덧셈 : 가수를 더함
3. 정규화 및 over/underflow 확인 : 결과를 1.xxx 형태로 조정
4. 반올림 & 재정규화 : 필요한 경우 반올림하고 다시 정규화

이 과정은 부호 처리, 언더플로우/오버플로우 검사 등을 포함해 매우 복잡하므로, 1클럭 사이클로는 처리할 수 없어 보통 여러 클럭 주기에 걸쳐 연산이 수행된다.

부동소수점 덧셈

1.000₂ × 2–1 + –1.110₂ × 2^-2 (0.5 + –0.4375)

1. 지수 정렬(align exponents)

• 두 숫자는 서로 다른 지수를 가지고 있으므로, 지수를 같게 만들어준다. 지수를 정렬하려면 지수가 더 작은 쪽(-2)을 더 큰 쪽(-1)에 맞춘다. 즉, 두 번째 수의 가수를 오른쪽으로 1비트 shift하면 된다.

–1.110₂ × 2⁻² → –0.1110₂ × 2⁻¹
정렬 : 1.000₍₂₎ × 2⁻¹  + (–0.1110₍₂₎ × 2⁻¹)

1. 가수 덧셈

• 이제 같은 지수이므로 가수끼리 직접 더할 수 있다.

1.000₂ + (–0.1110₂) = 0.0010₂

계산 결과 : 0.0010₂ × 2⁻¹

1. 정규화(Normalization)

• 부동소수점 표현에서는 결과가 항상 1.xxxx + 2^e의 형태로 표현되어야 한다.

0.0010₂ × 2⁻¹ → 정규화하면 → 1.000₂ × 2⁻⁴

• 가수를 왼쪽으로 3비트 shift -> 1.000₂ (over/underflow 없음)
• 지수는 그만큼 감소 -> –1 – 3 = –4

1. 반올림 및 정리

• 가수에 추가 비트가 없으므로 반올림은 필요 없다.

1.000₂ × 2⁻⁴ = 0.0625 (십진수)

FP Adder Hardware

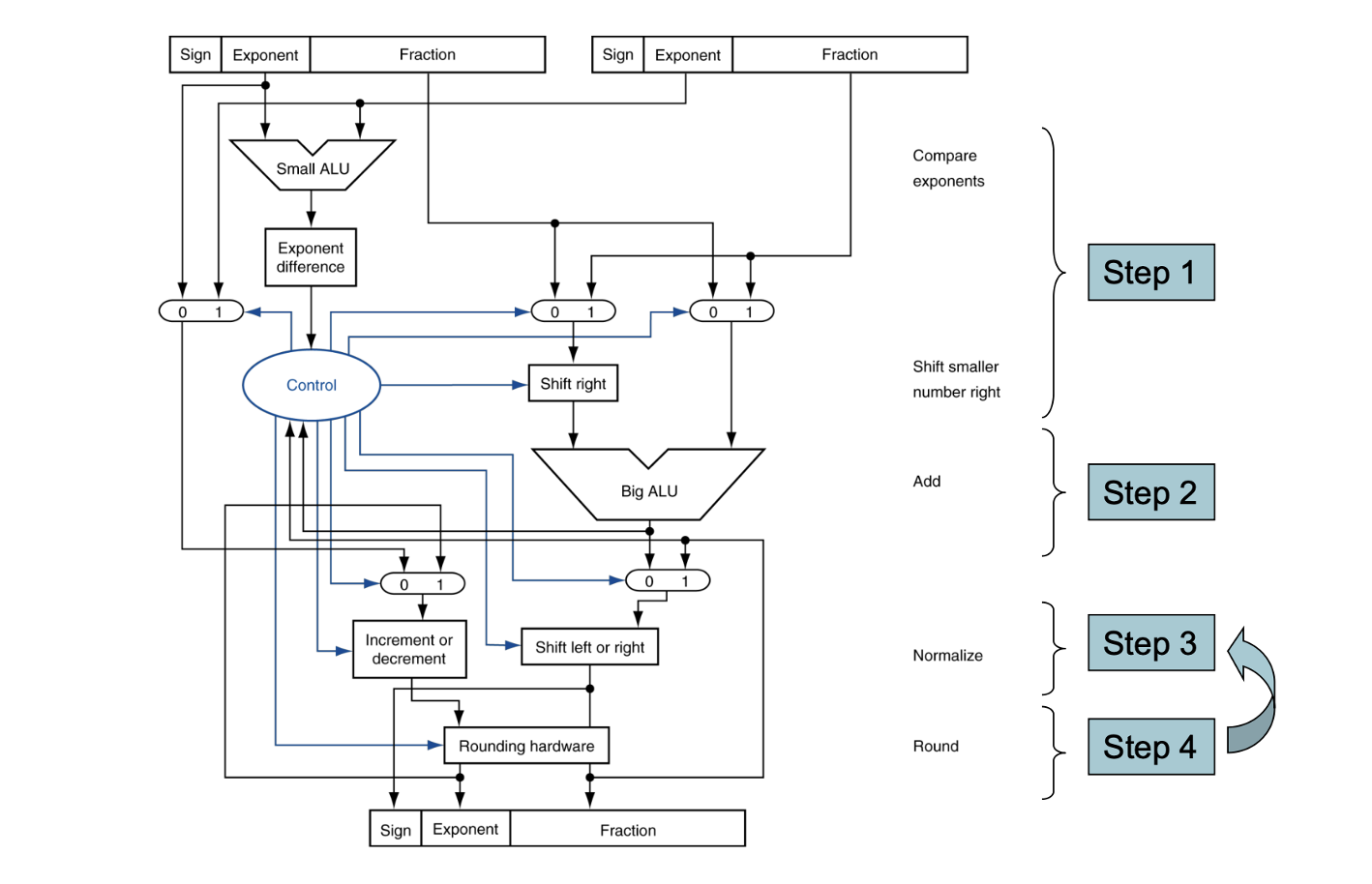
1. 지수 비교(Compare Exponents)
   • Small ALU : 두 입력의 지수 차이 계산
   • Exponent difference : 지수 차이를 제어 유닛에 전달
   • MUX : 더 작은 지수를 가진 입력을 감지 -> 그에 따라 가수를 shift
   • 동작 흐름
   1. 두 부동소수점 입력에서 Exponent 필드 추출
   2. Small ALU에서 E1 - E2 계산 -> 지수 차이 전달
   3. 지수가 더 작은 입력을 오른쪽으로 shift할 준비
   4. Control 유닛이 비교 결과에 따라 shift 제어선 활성화

• 목적
  • 가수끼리 제대로 덧셈하려면 지수를 일치시켜야함
  • 이를 위해 가수가 작은 쪽을 오른쪽으로 shift

1. 덧셈 or 뺄셈(Align & Add/Merge)
   • Shift Right : 작은 쪽 가수를 지수 차이만큼 오른쪽으로 shift
   • Big ALU : 가수끼리 더하거나 뺌
   • Control : 부호에 따라 덧셈/뺄셈 선택
   • 동작 흐름
   1. shift된 가수 + 큰 쪽 가수를 Big ALU로 전달
   2. 두 수의 부호가 같으면 덧셈, 다르면 뺄셈 수행
   3. 결과 가수는 다음 단계(정규화)로 전달
2. 정규화(Normalization)
   • Shift Left/Right : 결과 가수를 정규화(즉, 1.xxx 형태로 만들기)
   • Increment/Decrement : Shift 횟수만큼 지수도 조정
   • 동작 흐름
   1. 연산 결과 가수가 1.xxx 형태가 아니라면 shift 수행
   2. shift한 횟수만큼 Exponent 증가/감소
   3. 정규화된 결과를 다음 단계로 전달
3. 반올림(Rounding)
   • Rounding Hardware : Guard, Round, Sticky bits 검사 후 반올림
   • Final Sign/Exponent/Fraction 출력
   • 동작 흐름
   1. 정규화된 가수에서 추가 비트를 기준으로 반올림 여부 판단
   2. 필요시 가수 올림, 그에 따라 Exponent 조정
   3. 결과를 IEEE 754 형식으로 결합하여 출력
   4. 반올림 후 재정규화 필요시 다시 정규화로 돌아감

Control Units

Control 블록은 이 모든 흐름을 중앙에서 제어한다. ALU연산, Shift 방향, Mux 선택, Rounding 여부까지 모든 결정을 내린다.

• Small ALU : 비교 결과 수신
• Shift Right : 지수 차이만큼 작은 수 shift
• Big ALU : 덧셈 or 뺄셈 결정(부호 확인)
• Nomalize : shift 횟수 -> exponent 보정
• Round : 반올림 기준 판단 및 실행
• Write : 결과를 최종 출력