[데이터 통신] 오류 검출 및 수정 (Error Detection and Correction)

Introduction

우리가 데이터를 전송할 때, 중간에서 오류가 발생하는 것은 피할 수 없는 현실이다. 케이블의 잡음, 신호의 감쇠, 간섭 등 다양한 이유로 인해 데이터가 손상되거나 잘못 전달되는 일이 생긴다. 이번 페이지에서는 이러한 오류를 어떻게 검출(Detection)하고 수정(Correction)할 수 있는지를 다룬다.

오류의 종류와 Redundancy 개념 : 가장 먼저, 오류 제어의 기본이 되는 개념들을 소개한다. 단일 비트 오류(Single-bit error), 버스트 오류(Burst error) 등 여러 유형의 오류가 존재하며, 이를 막기 위해 redundancy(여분의 정보)를 추가하는 방법이 사용된다. 이러한 여분 정보는 원래의 데이터를 손상시키지 않으면서 오류를 감지하거나 수정할 수 있도록 도와준다. 이 부분에서는 오류를 ‘발견하는 것’과 ‘실제로 수정하는 것’의 차이점도 명확히 구분한다.

Block Coding과 Hamming Distance : 다음으로는 블록 코딩(Block Coding) 방식이 등장한다. 이는 데이터를 고정된 길이의 블록으로 나누고, 각 블록마다 오류 검출을 위한 코드를 추가하는 방식이다. 여기서 중요한 개념은 Hamming Distance(해밍 거리)이다. 두 코드워드 간의 해밍거리는 서로 다른 비트의 개수를 의미하며, 이를 통해 몇 개의 오류까지 감지하거나 수정할 수 있는지를 계산할 수 있다. 이 부분은 오류 제어의 ‘수학적 기반’을 이해하는데 핵심이 되는 내용이다.

Cyclic Codes와 CRC : 세 번째로 소개되는 것은 순환 코드(Cyclic Code)이다. 이는 블록 코딩보다 더 구조화된 방식으로, 특히 하드웨어적으로 구현하기 쉬운 장점이 있다. 순환 코드의 대표적인 예는 CRC(Cyclic Redundancy Check)이다. 우리가 자주 접하는 파일 다운로드 오류 검출, 네트워크 프레임 오류 체크 등에서 CRC는 거의 표준처럼 사용된다. CRC는 데이터를 다항식(polynomial)으로 표현하여 수학적으로 오류를 감지하는 방법이며, 매우 높은 검출 능력을 가지고 있다.

Checksums(체크섬) : CRC보다 조금 더 간단한 방식으로, 체크섬(Checksum)이 있다. 이는 주로 인터넷 프로토콜(IP)에서 사용되며, 여러 데이터 단위를 합산한 결과값을 통해 오류를 확인하는 방법이다. 여기서는 기본적으로 체크섬 계산뿐만 아니라, 전통적인 방식 외의 새로운 방법들도 소개된다. 예를 들어 1의 보수 기반 체크섬이나 가중치를 다르게 주는 방식도 언급된다.

Forward Error Correction(FEC) : 마지막으로는 오류 발생 이전에 미리 복구 가능한 정보까지 함께 보내는 방법, 즉 전방 오류 수정(Forward Error Correction, FEC)에 대해 다룬다. 이는 데이터가 손상되더라도 수신자가 스스로 복구할 수 있게 하는 방법으로, 실시간 통신(예: 스트리밍, 위성통신)에서 특히 중요하다. 이 파트에서는 해밍 거리 개념이 다시 활용되며, 그 외에도 비용이 덜 드는 방식들 - 예를 들면 패킷 XOR방식, interleaving, 고해상도 + 저해상도 결합 방법 등도 소개된다.

오류의 종류 (Types of Error)

데이터가 한 지점에서 다른 지점으로 전송되는 과정에서, 잡음(noise)이나 신호 간섭(interference) 등의 원인으로 인해 데이터가 손상될 수 있다. 이는 물리적인 매체의 한계이기도 하며, 데이터 통신에서 오류가 발생하는 가장 기본적인 이유이다.

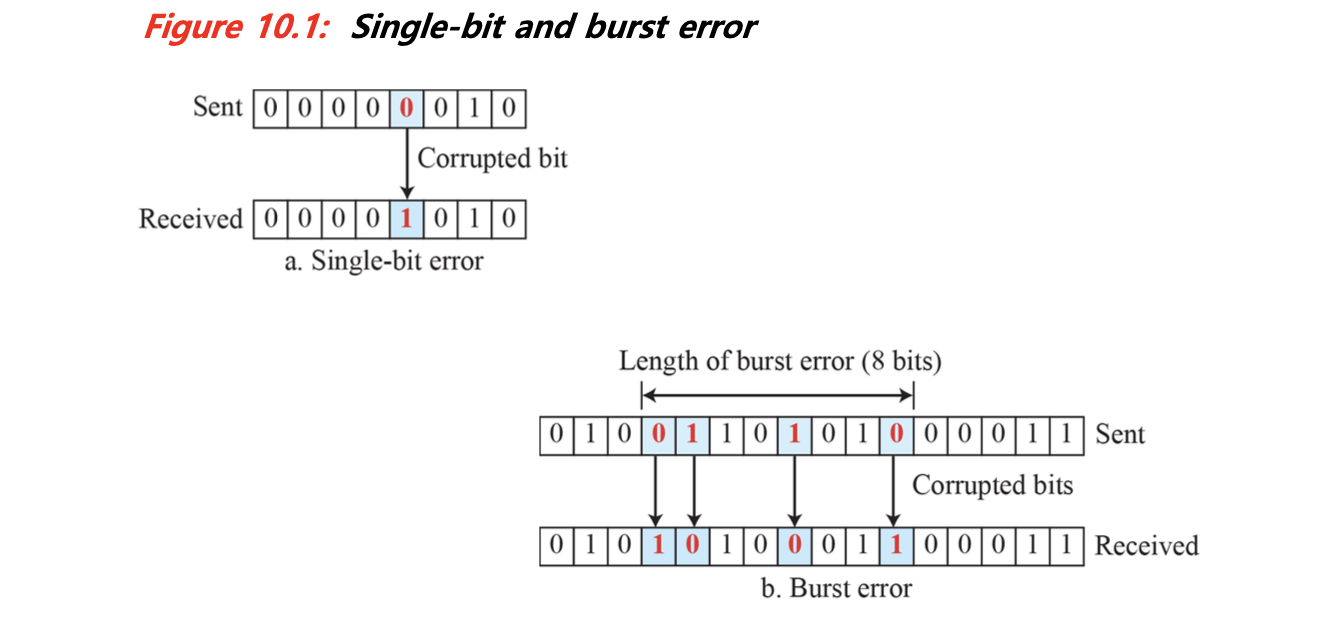
• Singl-bit-error(단일 비트 오류)란, 하나의 비트만 값이 뒤바뀌는 현상을 의미한다. 예를 들어, 1001001 이라는 7비트 데이터 중 가운데 하나의 비트가 0에서 1로 바뀌어 1001101 이 되는 것이 이에 해당한다.
• Burst error(버스트 오류)는 연속적으로 여러 비트가 손상되는 현상이다. 이때 연속된 오류는 서로 인접하지 않을 수 있으며, 일반적으로 최소 두 개 이상의 비트가 영향을 받는다. 예컨대 1001001dl 1011111로 바뀌는 경우 등이다.

실제 네트워크에서는 burst error가 더 흔하게 발생하며, 따라서 이에 대비한 더 강력한 오류 제어 메커니즘이 필요하다.

중복성 (Redundancy)

오류를 검출하거나 수정하기 위해, 우리는 전송 데이터에 불필요해 보이는 추가 정보(=Redundant Bias)를 함께 붙인다. 이 추가 정보는 수신자가 데이터를 분석할 수 있도록 해주며, 손상 여부를 파악하거나 실제 내용을 복구할 수 있는 단서를 제공한다.

• 송신자(sender)는 데이터를 전송하기 전에 이 redundant bit들을 추가한다.
• 수신자(receiver)는 데이터를 받은 후, 이 추가 정보를 분석하여 데이터의 무결성을 판단한다.

핵심은, 원래 데이터만으로는 오류를 파악할 수 없기 때문에, ‘여분 정보’가 반드시 필요하다는 것이다.

오류 검출 vs 오류 수정 (Detection vs Correction)

이 두 개념은 비슷해 보이지만, 목적과 난이도 측면에서 완전히 다르다.

• 오류 검출(Error Detection)은 단순히 데이터에 오류가 있었는지 Yes or No로 판단하는 것이다. 몇 비트가 손상되었는지는 중요하지 않고, 오류가 존재하면 거부(reject)하는 방식이다. 이 방법은 비용이 적고 구현이 간단하다.
• 오류 수정(Correction)은 오류가 발생한 정확한 위치를 파악하여, 원래의 데이터로 복원하는 것을 의미한다. 따라서 수신자는 손상된 비트의 개수와 위치를 모두 파악해야 하므로, 더 많은 정보와 복잡한 연산이 필요하다.

예를 들어 영상 스트리밍에서는 오류 검출 후 재전송을 요청하기 어렵기 때문에, 오류 수정 기법이 더 유용할 수 있다.

코딩을 통한 중복성 구현(Coding)

중복 비트를 데이터에 효율적으로 추가하려면, 체계적인 코딩 방법이 필요하다. 이러한 코딩 방식은 단순히 임의의 비트를 붙이는 것이 아니라, 데이터 비트와 수학적인 관계를 가지는 방식으로 redundant bit를 구성한다.

• 송신자는 데이터 비트와 중복 비트 사이의 수학적 관계를 만들어내고,
• 수신자는 이 관계를 검증하여 오류 유무를 판단한다.

이러한 코딩 방식의 종류, 중복 비트의 비율, 그리고 에러 검출/수정 능력(robustness)은 모두 오류 제어 설계에서 중요한 요소이다.

블록 코딩 (Block Coding)

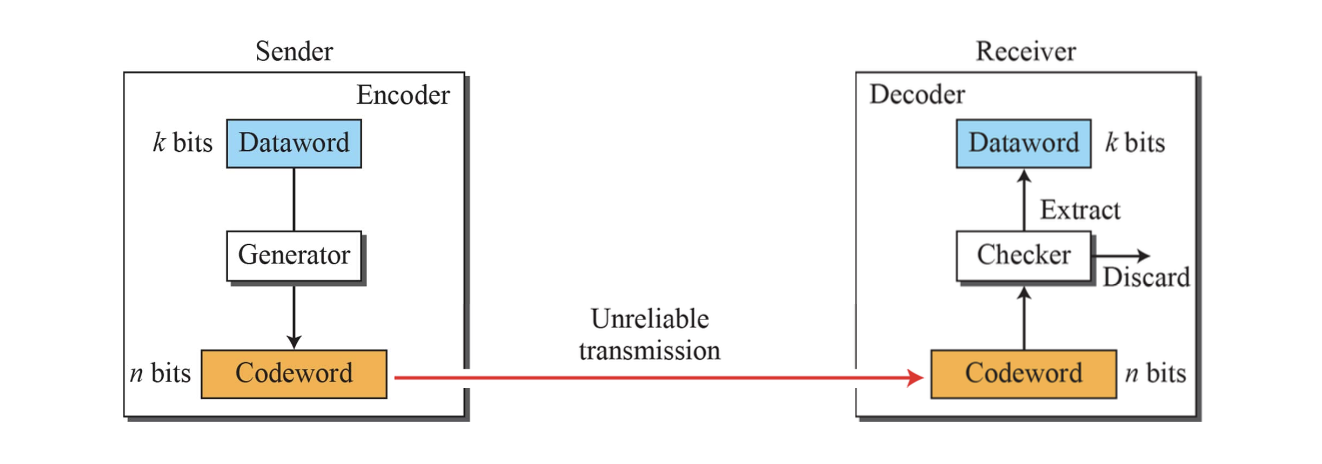
Block coding은 오류 검출/수정을 위한 기본적인 코딩 기법이다. 이 방식에서는 데이터를 일정 크기의 블록으로 나누어 처리한다.

• 원래 데이터 블록은 k비트이며, 이를 dataword(데이터 워드)라고 부른다.
• 여기에 r개의 redundant bit를 추가하여 총 n = k + r 비트의 새로운 블록을 생성하며, 이를 codeword(코드 워드)라고 부른다.

이러한 코드 워드는 전송 중에 오류가 발생하더라도, 수신자가 정해진 유효한 코드워드 리스트를 바탕으로 데이터의 무결성을 판단할 수 있게 한다.

Block Coding을 이용한 에러 검출 : 블록 코딩을 사용한 오류 검출의 핵심은 매우 직관적이다. 아래 두 가지 조건만 만족하면 오류가 있는지 확인할 수 있다.

• 수신자가 유효한 코드워드 목록(또는 생성 방법)을 가지고 있어야 한다.
• 수신된 데이터가 이 목록에 포함되지 않는 경우, 오류가 발생한 것으로 판단할 수 있다.

이 방식은 해밍 거리(Hamming Distance)와 밀접한 관련이 있으며, codeword 간 최소 해밍 거리를 기반으로, 몇 개의 오류까지 검출 또는 수정 가능한지를 판단하게 된다. 예를 들어, 최소 해밍 거리가 3이라면 1비트 오류는 무조건 검출이 가능하다는 의미이다.

Example

• Example1 : 기본 블록 코드 예시
  • 조건 : k = 2(dataword 길이 2비트), n = 3(codeword 길이 3비트)
  • 설명 :
    • 가능한 2비트 dataword는 총 4개: 00 01 10 11
    • 각 dataword에 대해 1비트의 패리티 비트를 추가해서 3비트 codeword를 만든다.

• Example2 : 해밍 거리 계산
  • 설명 :
    • 해밍 거리는 두 비트열의 같은 자리에서 다른 비트의 개수
    • 101과 001의 해밍 거리 : 1 (첫 번째 비트만 다르다.)
    • 101과 010의 해밍 거리 : 3 (모두 다름)
  • 공식 :
    • s개의 오류를 확실히 검출하려면 : d_min = s + 1
• Example3 : d_min 확인
  • 위 테이블 코드의 최소 해밍 거리 : d_min = 2
  • 이 코든 1비트 오류까지는 확실히 검출 가능
  • 2비트 오류 발생 시, 다른 유효한 codeword로 바뀔 수 있으므로 오류 검출 실패 가능
• Example4 : d_min = 4 인 경우
  • 해밍 거리 d_min = 4
  • 이 코드는 최대 3비트 오류까지 확실히 검출 가능
  • d_min = s + 1 => s = d_min - 1 = 3
• Example5 : 선형 블록 코드 여부 확인
  • 검증 방법 :
    • 어떤 두 개의 codeword를 XOR 했을 때, 결과가 또 다른 유효한 codeword면 선형블록코드
  • 예시(위 테이블 기준) :
    • 두 번째 codeword XOR 세번째 codeword = 네번째 codeword
  • 결론
    • 위 Table은 선형 블록 코드
• Example6 : 1의 개수와 d_min 확인
  • 위 테이블의 non-zero codeword들의 1의 개수는 모두 2개
  • 이 말은, 서로 다른 codeword 사이 최소 해밍 거리가 2라는 의미
  • d_min = 2
• Example6 + : Simple Parity - Check Code C(5, 4)

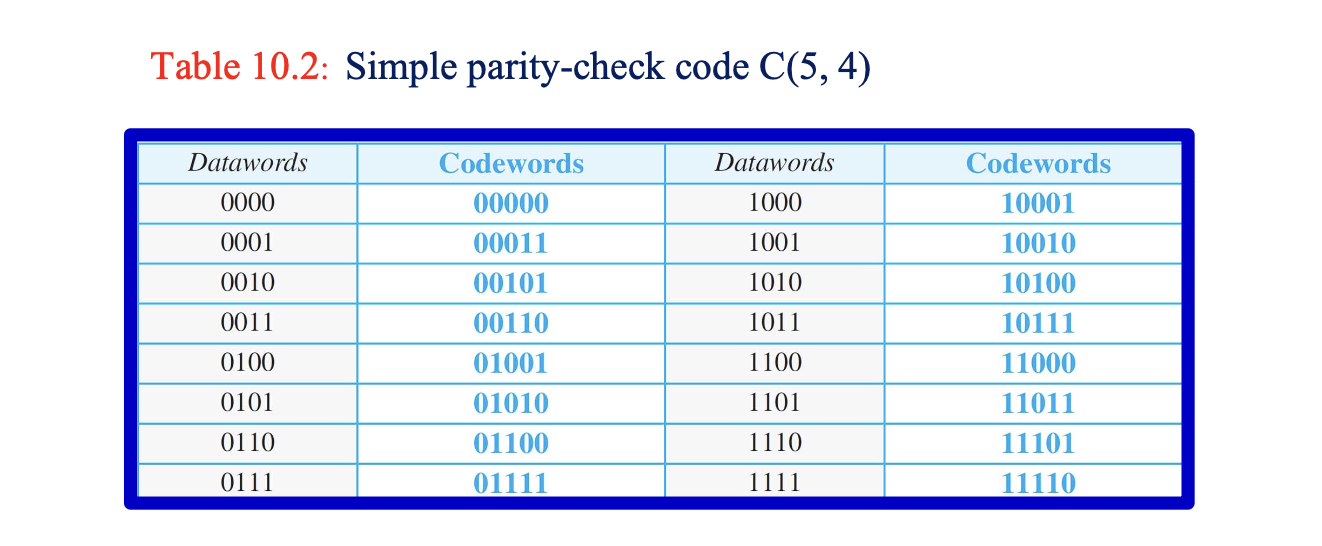
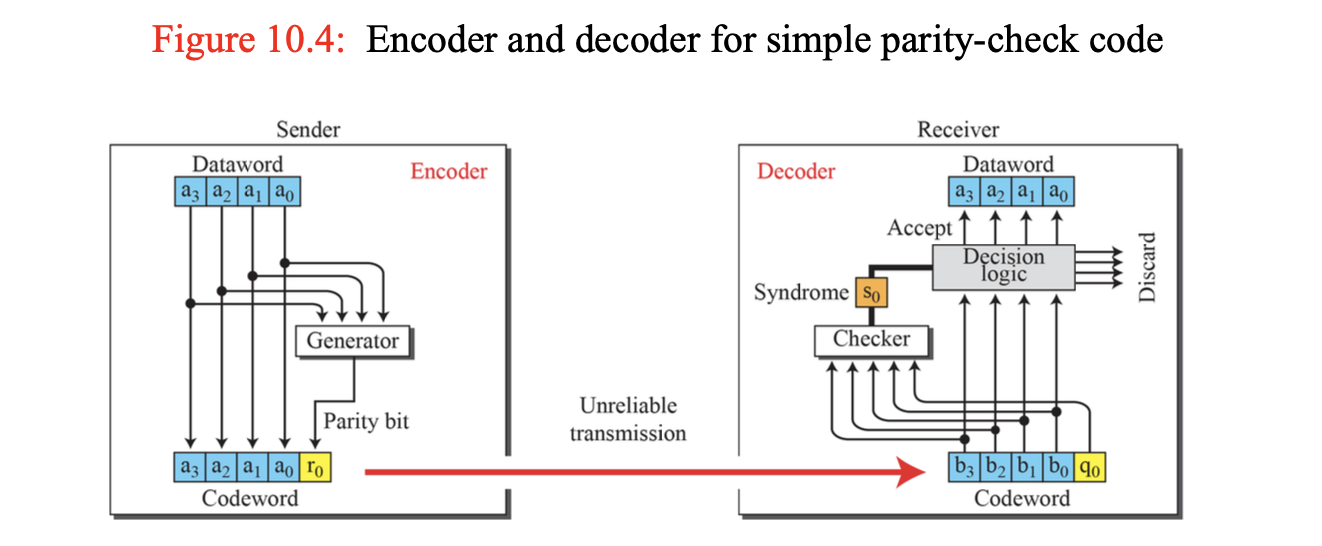
• 홀수 개의 1이 있는 경우에 오류 검출 가능
• 짝수 개의 오류는 감지 불가능할 수도 있음

Cyclic Codes - 순환 코드의 개념과 CRC

우리가 앞에서 살펴본 Block Coding은 데이터에 여분의 비트를 추가해 오류를 검출하거나 수정할 수 있게 해주는 방식이다. 이번 페이지에서는 이러한 Block coding 중에서도 특벌한 구조적 성질을 갖는 순환 코드(Cyclic Codes)에 대해 알아본다. 순환 코드는 오류 검출 능력이 뛰어나면서도 하드웨어 적으로 쉽게 구현 가능한 장점 덕분에, 실제 네트워크 시스템에서 매우 자주 활용된다.

Cyclic Redundancy Check (CRC)

순환 코드는 선형 블록 코드(Linear block code)의 일종이지만, 한 가지 독특한 특성이 있다. 어떤 코드워드 왼쪽이나 오른쪽으로 순환 시프트(cyclic shift)하더라도, 여전히 유효한 코드워드라는 점이다. 예를 들어 1011000 이라는 코드워드를 왼쪽으로 순환시키면 0110001이 되며, 이 또한 유효한 코드워드로 인정된다. 이러한 성질은 순환 코드의 구조적 규칙성과 관련되어 있으며, 오류 검출 과정에서 큰 장점이 된다.

특히, 순환 코드 중에서 가장 널리 알려진 방식이 바로 CRC(Cyclic Redundancy Check)이다. CRC는 LAN, WAN, USB, Bluetooth, 저장 장치 등 다양한 네트워크 및 디지털 시스템에서 표준처럼 사용된다.

CRC는 단순히 데이터를 나누는 방식이 아니라, 데이터를 이진 다항식(Binary Polynomial)으로 표현하고 수학적 연산을 통해 오류를 검출하는 구조이다.

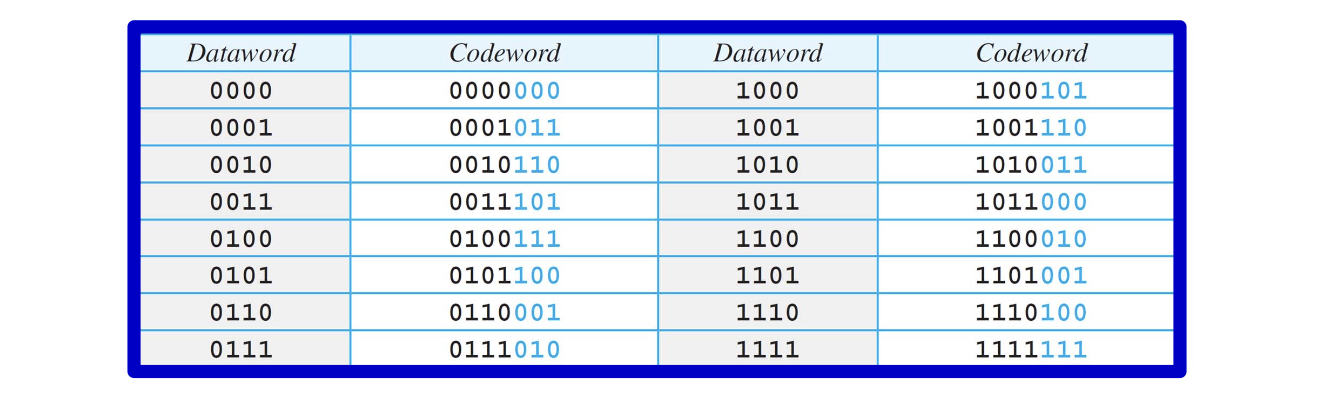
• C(7, 4) : block code 형식을 의미, 각 데이터워드는 4비트(k=4), 각 코드워드는 7비트(n=7). 즉, 4비트의 데이터 + 3비트의 CRC(또는 패리티) 비트를 붙여서 총 7비트로 만든 것이다.
• 위에 표는 모든 가능한 4비트 데이터워드(0000~1111)에 대해, 각각 어떤 7비트 codeword가 매핑되는지를 보여주는 것이다. 즉, dataword -> codeword로 인코딩된 결과를 나열한 것이다.
• 위와 같은 코드가 필요한 이유? : 전송 중 오류가 발생했을 때, 수신자가 올바른 codeword만을 알고 있다면, 수신된 데이터가 오류가 있는지 없는지 판단할 수 있다. 예를 들어, 0010110이라는 7비트가 도착했는데, 이게 유효한 codeword 목록에 있다면 오류가 없다고 판단한다. 하지만 이와 다른 어떤 7비트 조합이 도착했다면, 오류가 발생했다고 판단할 수 있다.

Polynomials - 이진 다항식 표현

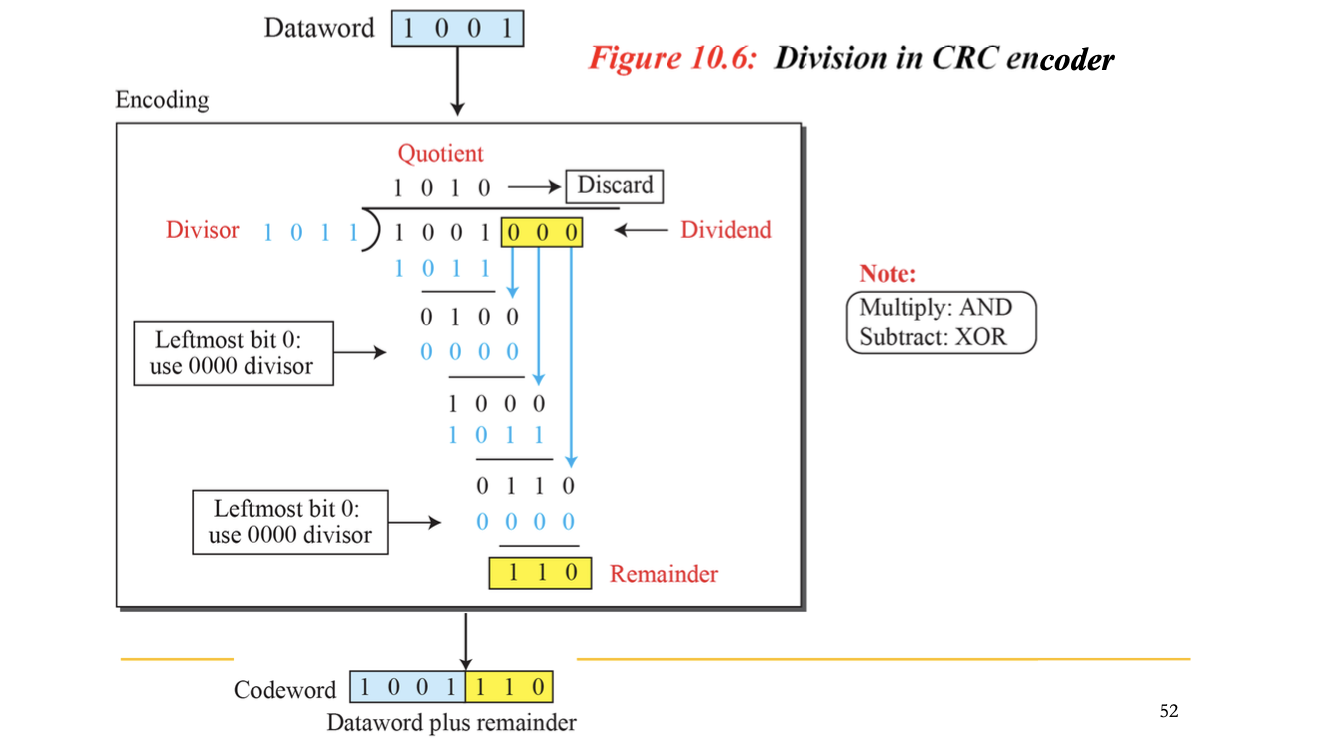
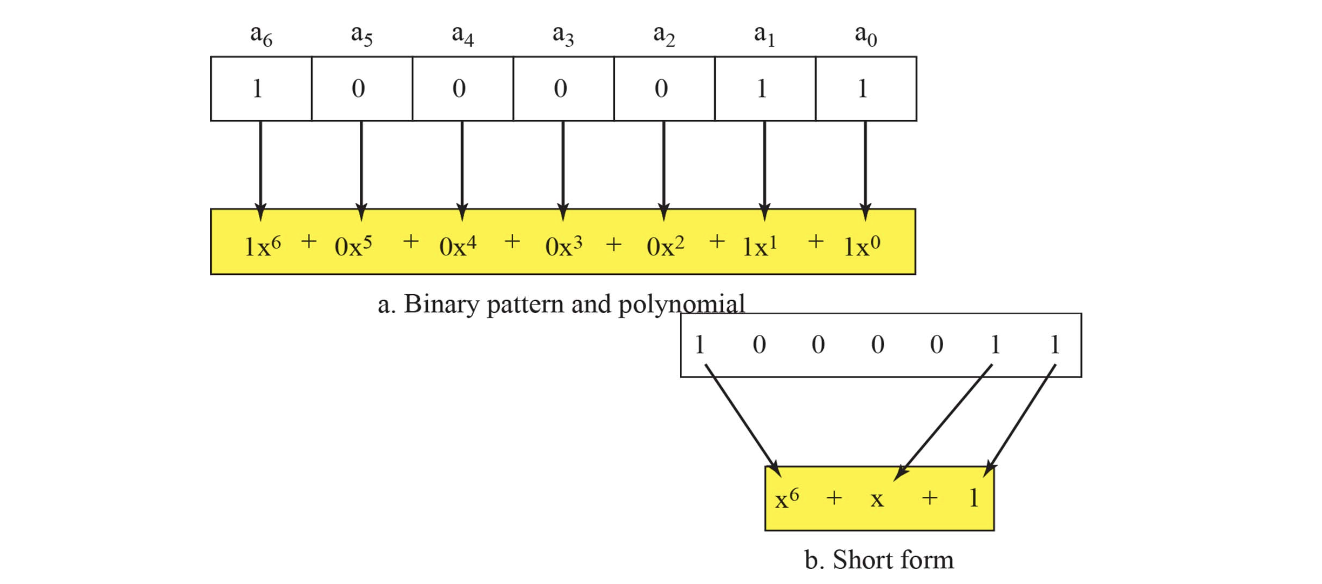
CRC에서의 핵심은 데이터를 단순한 비트열이 아니라 이진 다항식으로 보는 것이다. 예를 들어 1101 이라는 비트열은 다항식으로는 x³ + x² + 1로 표현된다.

• 각 비트의 위치(index)는 다항식의 차수(degree)로,
• 각 비트의 값(0 또는 1)은 다항식의 계수(coefficient)로 사용된다.

이러한 표현 방식은 나눗셈 연산을 통해 CRC 코드를 생성하거나 오류를 검출하는 데 매우 효과적이다.

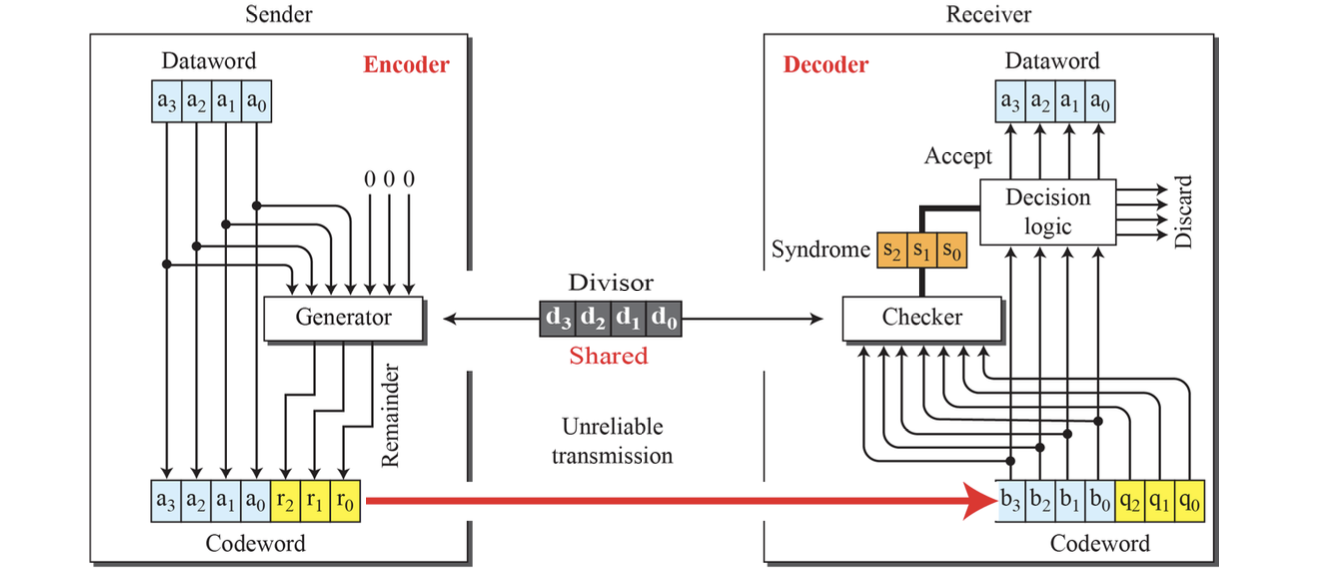
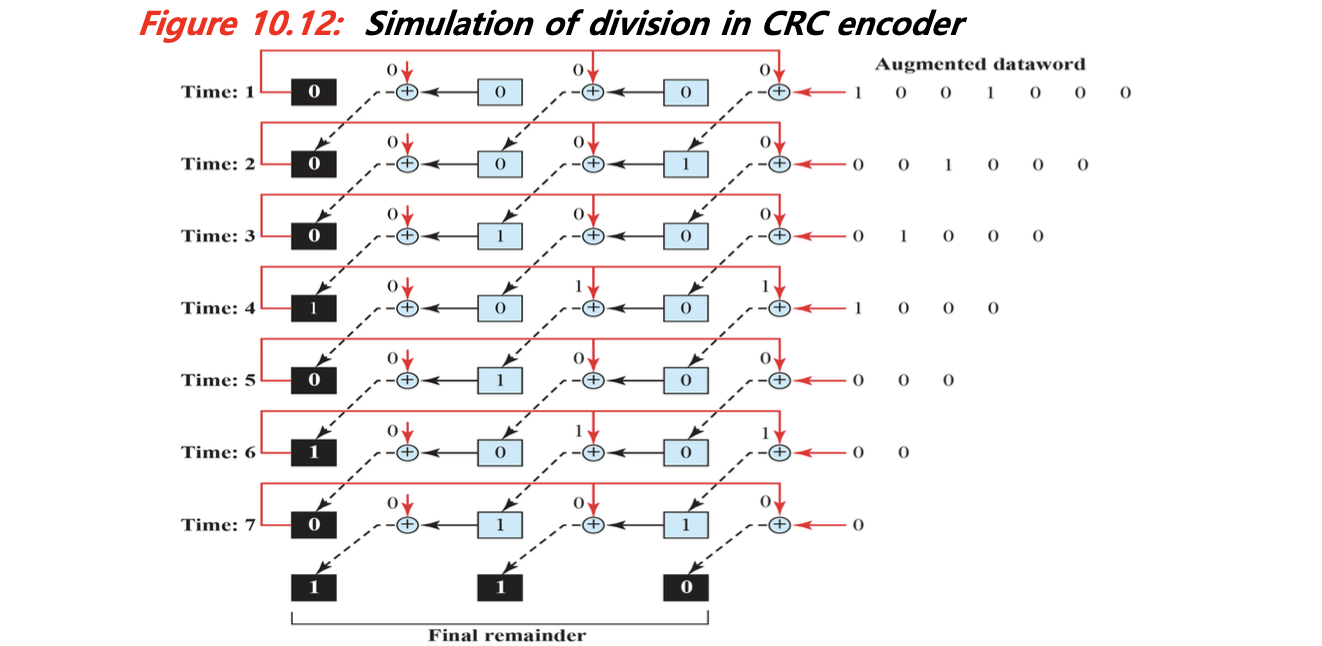
Encoder Using Polynomials - 인코딩 방식

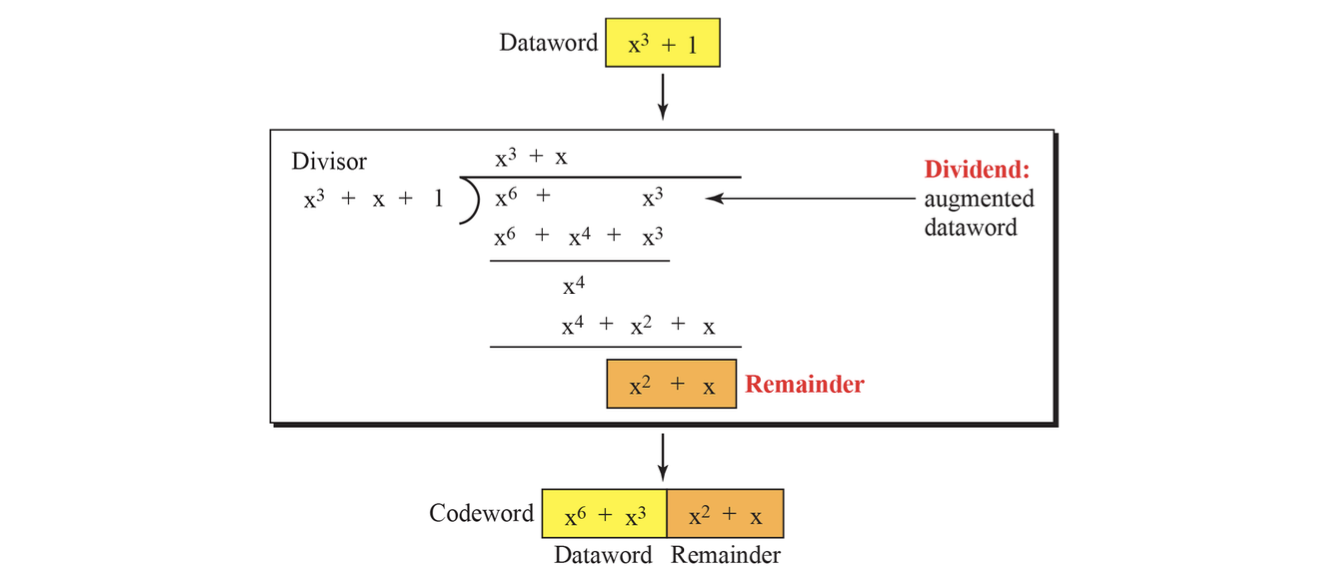
CRC 인코딩 과정은 다음과 같은 절차로 진행된다.

• 송신자는 데이터 워드 D(x)에 0을 r개 붙여 임시 다항식을 만든다.
• 이 임시 다항식을 제너레이터 G(x)로 나눈다.
• 나머지 R(x)를 계산하고, 이 값을 원래 데이터 뒤에 붙여서 코드워드 C(x) = D(x) + x^r + R(x)를 완성한다. 이 과정은 이진 나눗셈(Binary Division) 방식으로 수행되며, 그림으로 표현된 시프트 레지스터(Shift Register)를 통해 하드웨어적으로도 구현 가능하다.

CRC에서 제너레이터 G(x)는 매우 중요한 역할을 하며, 특정 종류의 오류를 얼마나 잘 검출할 수 있을지를 결정한다.

Cyclic Code 분석 및 오류 검출 능력

이제 CRC가 얼마나 효과적으로 오류를 검출할 수 있는지 살펴봐보자. CRC는 다음과 같은 오류를 매우 잘 검출할 수 있다.

• 단일 비트 오류(Single-bit error)
• 이중 비트 오류(Double-bit error)
• 홀수 개의 비트 오류(Odd number of bit errors)
• 버스트 오류(Burst error)

CRC의 검출 능력은 사용하는 제너레이터 다항식 G(x)의 성질에 달려 있으며, 보통 다음과 같은 조건이 충족될 때 매우 강력한 오류 검출이 가능하다.

• G(x)의 계수 중 x⁰(상수항)이 반드시 1이어야 한다.
• G(x)가 (x^t + 1)을 나누지 못한다면, t길이 이하의 burst 오류를 모두 검출할 수 있다.

CRC 코드 분석

• 다항식 f(x)와 오류 패턴 : 모든 오류 패턴은 다항식으로 표현할 수 있다. 예를 들어, 단일 비트 오류는 다음처럼 표현된다. E(x) = x^t(t번째 비트에 오류가 났다는 뜻). 이때 우리가 사용하는 생성 다항식(Generator Polynomial), g(x)가 이 E(x)를 나눌 수 없다면, 오류는 검출된다.

• 핵심 조건1 : 모든 단일 비트 오류 검출 조건 : 생성 다항식 g(x)가 두 개 이상의 항을 가져야 하며, 상수항 x⁰의 계수 = 1이면, 모든 단일 비트 오류를 검출할 수 있다.
• 예: g(x) = x + 1은 조건 만족 -> 단일 비트 오류 검출 가능

• a. x+1 -> 검출 가능(두 항, 상수항 1)
• b. x³ -> 상수항 없음, 불가능

• c. 1 -> 항이 하나뿐, 검출 불가능

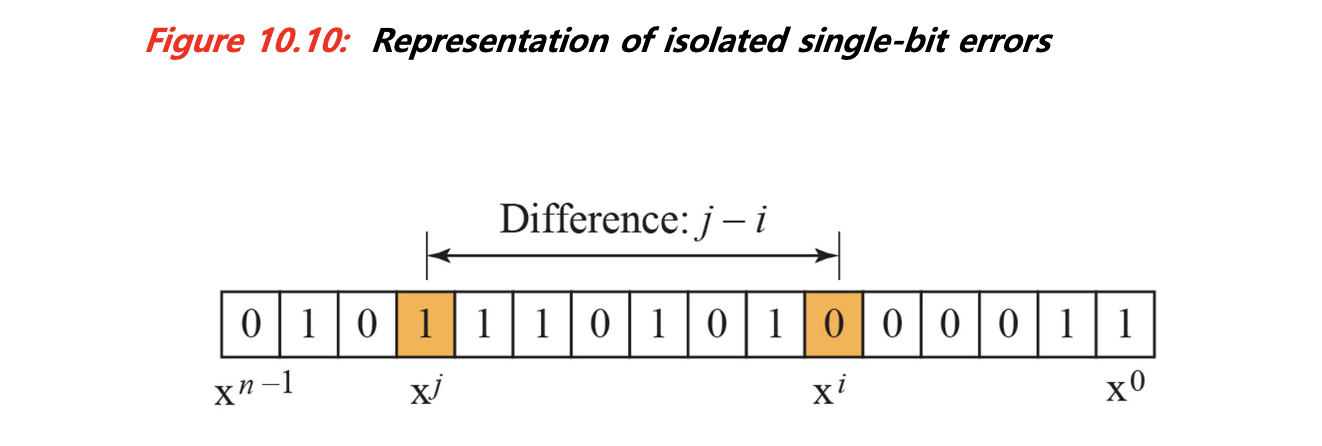
• 모든 isolated 오류 검출 조건 : 모든 isolated t비트 오류를 검출하려면 다음 조건을 만족해야 한다.
  • 생성 다항식 g(x)가 x^t + 1 을 나눌 수 없어야 함 (t=0 ~ t=n-1)
  • 이 조건을 통해 두 비트 이상 떨어진 오류도 잡아낼 수 있는지 판단 가능하다.

• a. x + 1 => 검출 불가능, x + 1은 xᵗ + 1을 나누는 경우 존재 → 일부 2비트 오류 검출 불가
• b. x⁴ + 1 => 검출 불가능, x⁴ + 1은 xᵗ + 1을 나눌 수 있음
• c. x⁷ + x⁶ + 1 => 검출 가능, 충분히 복잡한 형태, xᵗ + 1을 나누지 않음
• d. x¹⁵ + x¹⁴ + 1 => 검출 가능, 고차항, 검출력 매우 높음

CRC의 장점

• 다양한 유형의 오류를 높은 확률로 검출 가능하다.
• 하드웨어 및 소프트웨어 모두에서 간단하게 구현이 가능하다.
• 연산 속도가 빠르며, 실시간 처리가 가능하다.
• 구현 시 비교적 비용이 적게 든다.

기타 Cylic code

우리가 다룬 CRC는 순환 코드 중에서도 비교적 단순한 형태에 속한다. 하지만 실제로는 Galois Field(갈루아 체)와 같은 추상 대수학적 개념을 활용하여 더 강력한 순환 코드가 존재한다.

가장 대표적인 것이 Read-Solomon Code이며, 이는 DVD, QR코드, 위성 통신, 5G 네트워크 등에서 오류 검출뿐 아니라 수정 기능까지 포함하여 활용되고 있다.

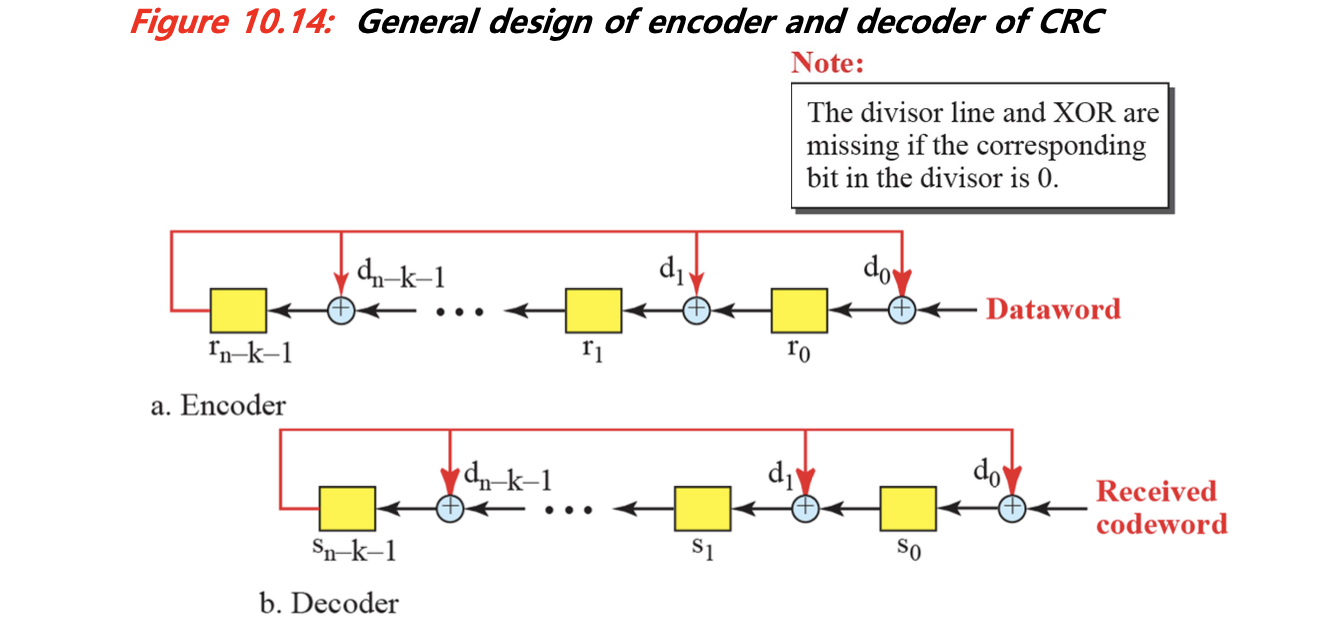
하드웨어 구현

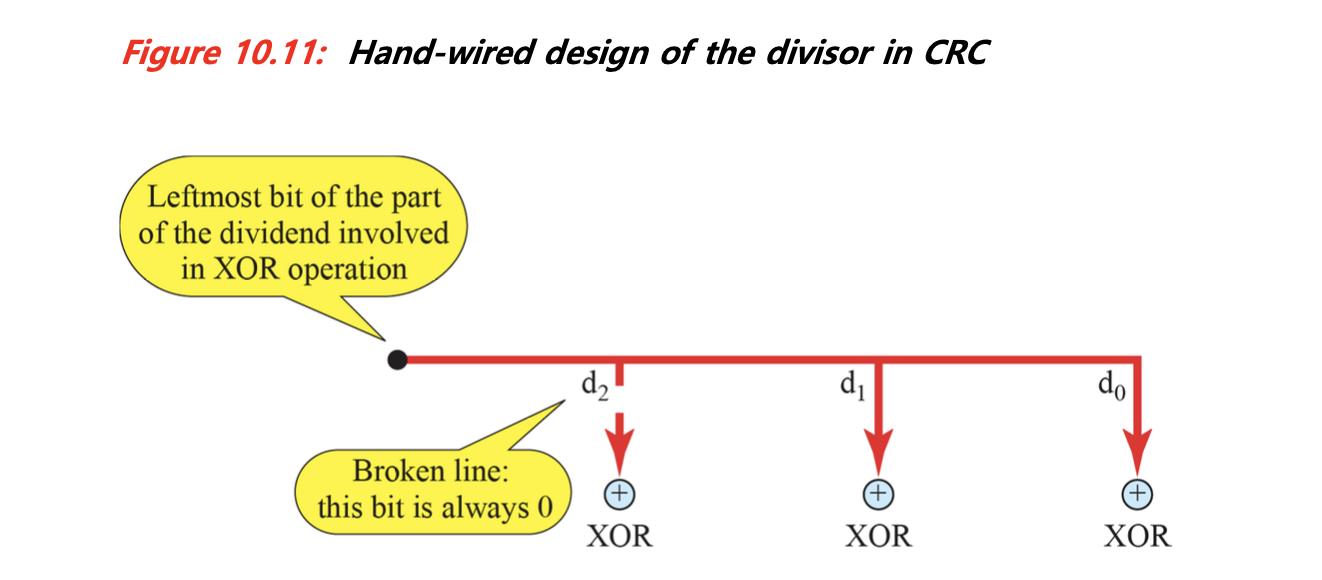
마지막으로 CRC의 또 다른 강점인 하드웨어 기반 구현에 대해 소개한다. 실제 회로 설계에서는 다음과 같은 방식으로 구현된다.

• AND, XOR, Shift Register 등 간단한 논리 회로만으로 구성 가능
• 송신기에서는 CRC 코드 생성, 수신기에서는 syndrome 계산을 통해 오류 검출
• 회로 크기가 작고, 속도가 빠르기 때문에 임베디드 시스템이나 네트워크 카드 등에 이상적이다.

Checksum - 전송 오류를 간단히 잡아내는 검출 기법

우리가 앞에서 살펴본 CRC나 블록코딩은 정교한 수학적 구조를 활용해 오류를 검출하는 방법이었다. 이번에 배울 체크섬(Checksum)은 그에 비해 훨씬 간단한 방식으로 오류를 검출하는 기법이다. 특히 인터넷에서는 이 방식이 네트워크 계층과 전송 계층에서 주로 사용된다.

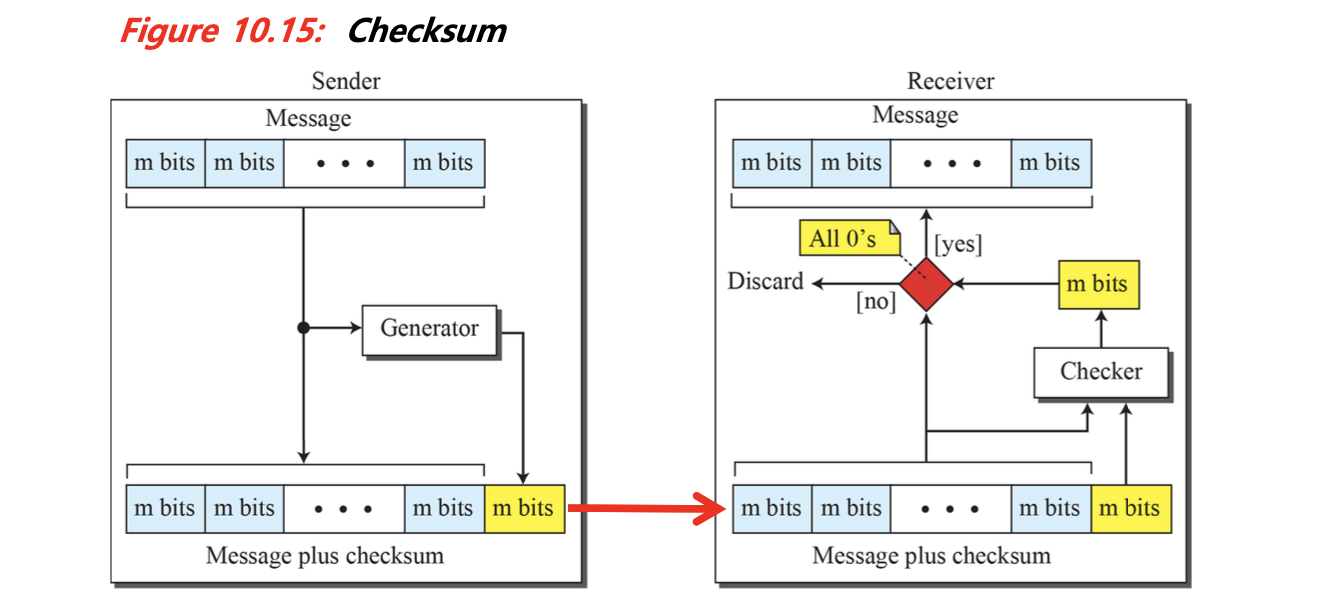
Checksum의 기본 개념

체크섬의 기본 아이디어는 단순하다. 여러 개의 숫자(데이터)를 전송할 때, 이 숫자들의 합계(sum)를 함께 전송한다. 수신자는 받은 숫자들을 다시 더해서, 체크섬으로 받은 값과 일치하는지 확인한다. 만약 같지 않다면 오류가 발생한 것으로 판단한다.

• 예시: Decimal 방식
  • 전송할 숫자 : (7, 11, 12, 0, 6)
  • 합계 : 7 + 11 + 12 + 0 + 6 = 36
  • 송신자는 7, 11, 12, 0, 6, 36을 보낸다.
  • 수신자는 앞의 다섯 개를 더해보고, 마지막 체크섬과 비교한다.

이 방식은 이해가기 쉽고 빠르게 구현할 수 있지만, 아직 이진 기반 시스템에 맞춘 처리 방식은 아니다.

체크섬을 이진(Binary) 방식으로 전환

위 예시에서 사용한 36은 이진수로 100100이다. 하지만 체크섬에서는 일반적으로 고정 비트수(예: 4비트)를 사용하기 때문에, 초과된 비트는 다음과 같이 처리한다.

• 초과된 왼쪽 비트(1)를 오른쪽에 더해주면 0010 + 1 = 0011 처럼 되는 “wrap-around carry” 방식

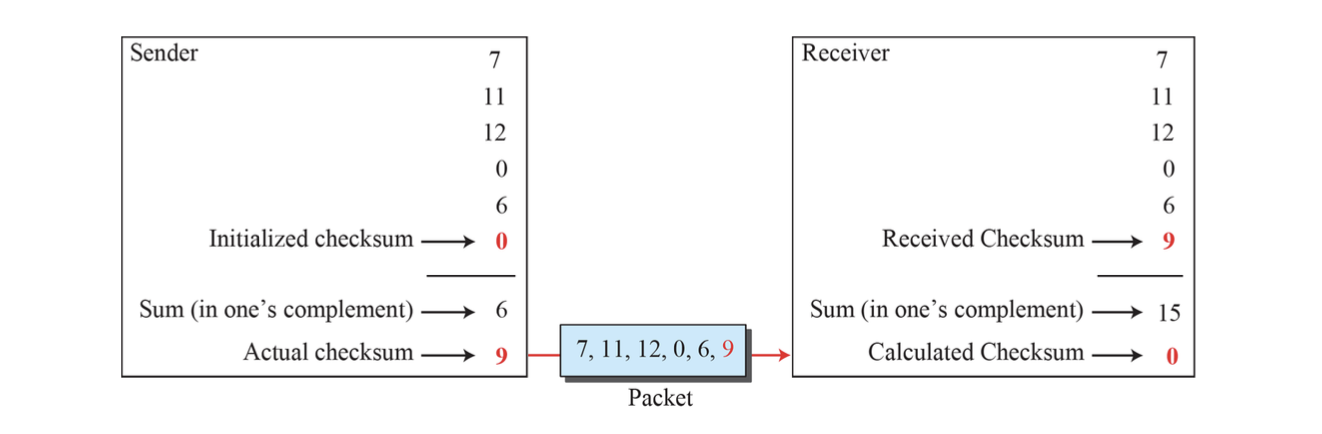
• 그리고 체크섬은 단순한 합계가 아닌, 1의 보수(One’s Complement) 연산을 적용한다.

• 프로세스 :
  • 다섯 개 숫자를 1의 보수 연산으로 더한다.
  • 합계를 다시 1의 보수 처리하여 체크섬을 생성 checksum = 9 (15 - 9)
  • 전송 데이터 : 7, 11, 12, 0, 6, checksum(=9)
  • 수신자는 받은 6개 수를 1의 보수 연산으로 합산
  • 결과가 1111(=15)이면 오류 없음

이 방식은 오류 검출력을 어느 정도 확보하면서도 계산이 간단해서 UDP, IP 헤더 등에서 실제로 사용된다.

체크섬 계산 절차 요약

1. 데이터를 고정된 단위(예: 4비트 또는 16비트)로 나눔
2. 1의 보수 연산으로 모든 블록을 더함
3. 결과값의 1의 보수를 취함
4. 그 값을 체크섬으로 전송
5. 수신자는 전체(데이터 + 체크섬)을 다시 1의 보수 연산으로 더해 결과가 전부 1이면 오류 없음으로 판단

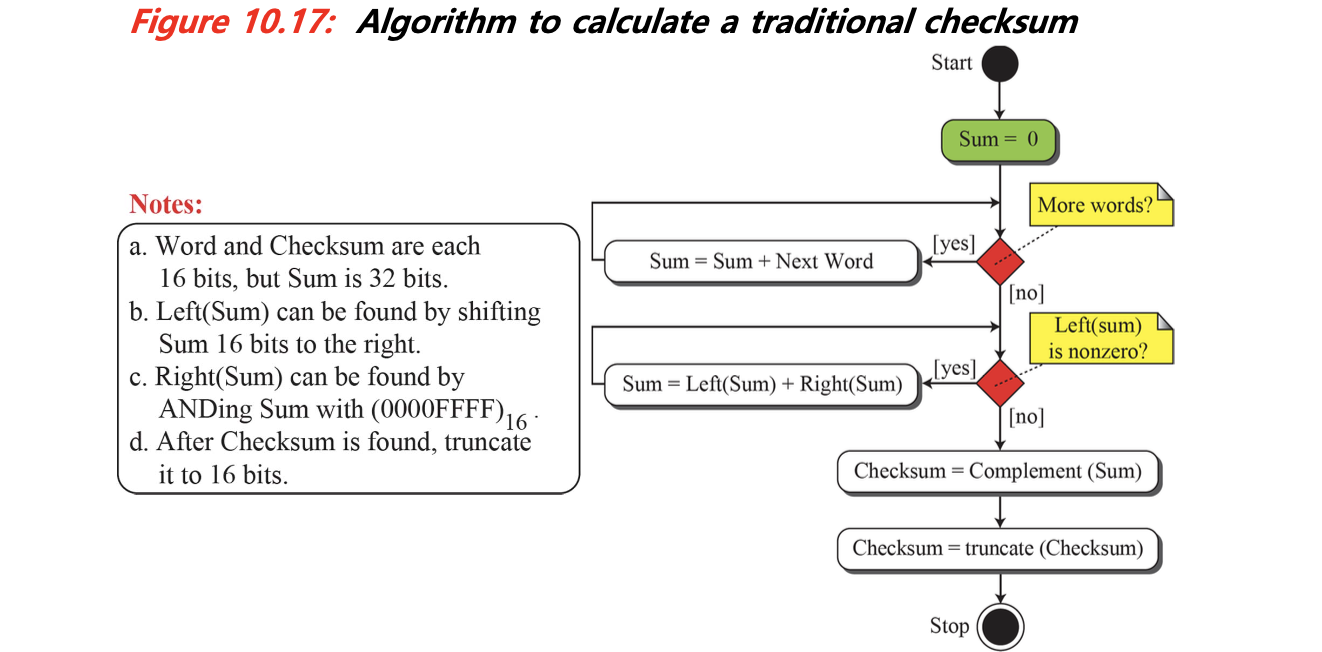
다른 체크섬 방식들(Fletcher, Adler)

전통적인 체크섬에는 중요한 약점이 있다. 데이터의 순서가 바뀌어도 오류를 감지하지 못할 수 있다. 왜냐하면 전통 체크섬은 순서에 가중치를 두지 않기 때문이다. 예를 들어 16비트 단위 데이터를 A, B로 전송했는데 B, A로 바뀌어도 합계는 같을 수 있기 때문인다. 이를 보완하기 위한 방법 들이 있다.

• Fletcher CheckSum
  • 각 데이터 블록에 위치에 따른 가중치를 부여한다.
  • 두 개의 누적 합(sum1, sum2)을 사용해 계산하며,
  • 결과적으로 데이터 순서 변화에 민감해진다.

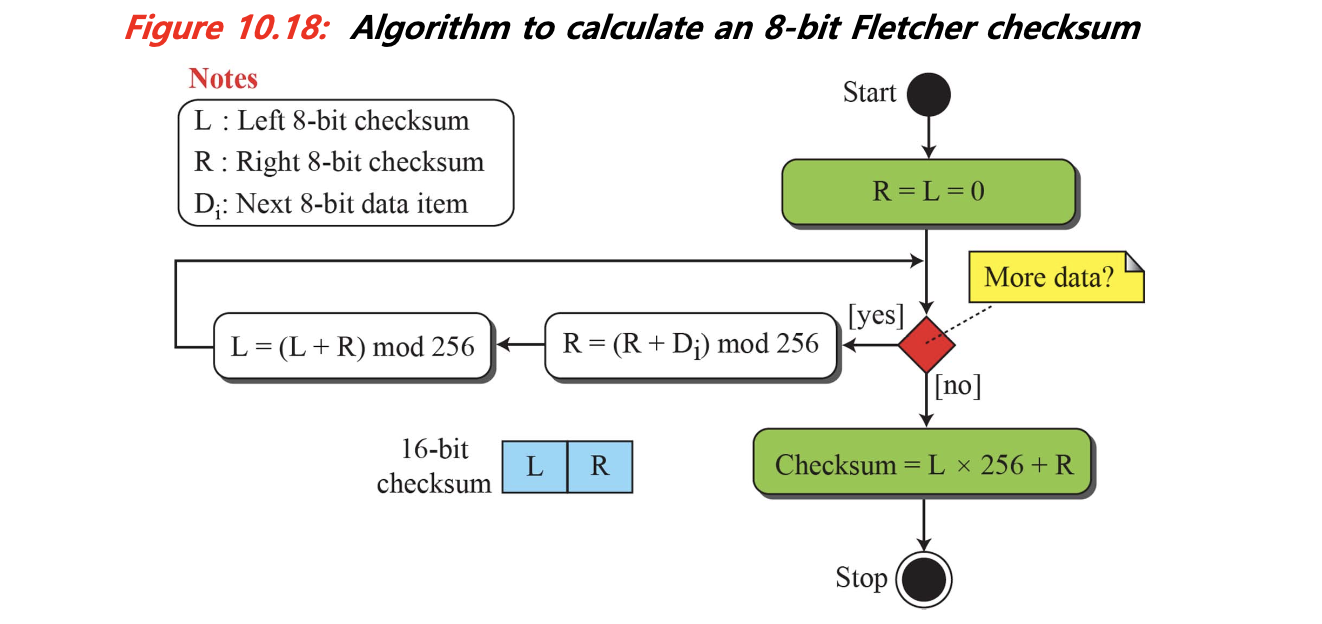
• Alder Checksum
  • Fletcher의 아이디어를 확장하여 속도와 정확성을 개선한 방식이다.
  • 일반적으로 Adler-32 형식으로 쓰이며, zlib 등에서 사용된다.

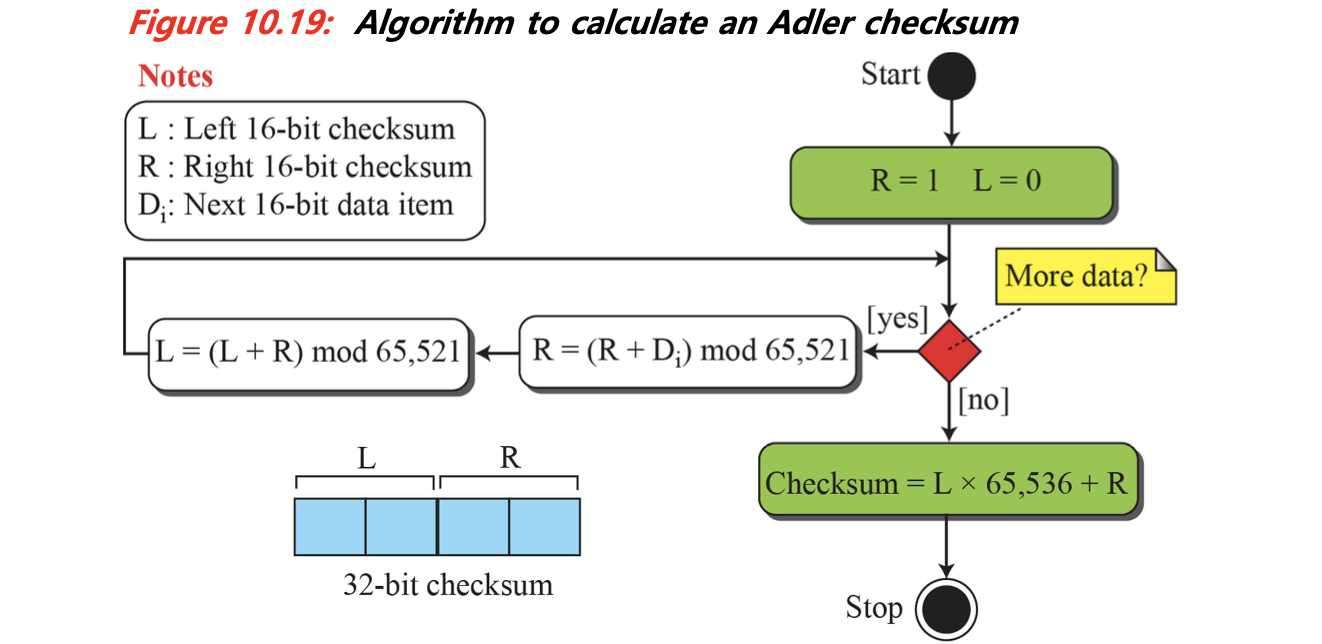
두 방식 모두 전통 체크섬보다 복잡하지만, 순서 변경이나 더 복잡한 오류에 대해 더 강력한 검출 능력을 가진다.

Forward Error Correction - 오류를 미리 고치는 지능적인 방식

이전까지는 오류가 발생했을 때 검출(detection) 후 재전송(retransmission)하는 방식이 중심이었다. 하지만 실시간 멀티미디어 통신(영상, 음성 스트리밍 등)에서는 패킷이 손상되었다고 매번 다시 요청하기엔 시간이 너무 오래 걸린다.

따라서 여기서는 수신자가 재전송 없이, 스스로 오류를 복구할 수 있도록 데이터를 구성하는 방식인 Forward Error Correction(FEC)을 다룬다. FEC는 데이터를 보낼 때부퉈 복구웨 필요한 여분 정보를 함께 보내는 방식이다.

해밍 거리(Hamming Distance)를 이용한 오류 수정

앞서 해밍 거리는 오류를 검출하는 데 사용되었지만, 이번에는 수정에도 사용하는 방법을 소개한다.

• 오류 t개를 수정하려면, 최소 해밍 거리 d_min이 2t + 1 이상이어야 한다.
• 예를 들어, 한 패킷에서 10개의 비트 오류를 수정하려면 해밍 거리가 최소 21이 되어야 한다.
• 이 말은, 오류를 수정하려면 많은 양의 중복 정보(redundancy)가 필요하다는 의미이다.

이 개념은 구형(구슬 모양)의 비유로 설명이 가능하다. 각 코드워드를 중심으로 반지름이 t인 구를 그렸을 때, 이 구들이 서로 겹치지 않도록 거리를 유지하면서 수신자는 어떤 구 안에 들어있는지만으로 원래 코드워드를 알아낼 수 있다.

XOR 연산을 활용한 간단한 복구 방식

또 하나의 간단한 FEC 아이디어는 XOR연산을 이용하는 것이다. 예를 들어, 세 개의 패킷 A, B, C를 보낼 때:

• 보조 패킷 D = A ⊕ B ⊕ C 를 생성
• 수신자 A나 B나 C 중 하나를 잃어버렸다면, 나머지 두 개와 D를 XOR해서 잃어버린 것을 복원 가능하다. (예: 예: C = A ⊕ B ⊕ D)

청크 인터리빙(Chunk Interleaving)

또 다른 방식은 데이터를 청크(Chunk) 단위로 나눠서 순서를 섞어(interleaving) 전송하는 것이다.

• 멀티미디어 전송에서는 일부 청크가 손실되더라도 전체 품질에는 큰 영향이 없는 경우가 많다.
• 따라서 하나의 패킷에 있는 모든 청크가 사라지는 것을 방지하는 것이 중요하다.

이 방식을 사용하면, burst error도 데이터 전체가 아닌 여러 패킷에 분산되기 때문에 복구 가능한 손실로 바꿔주는 효과가 있다.

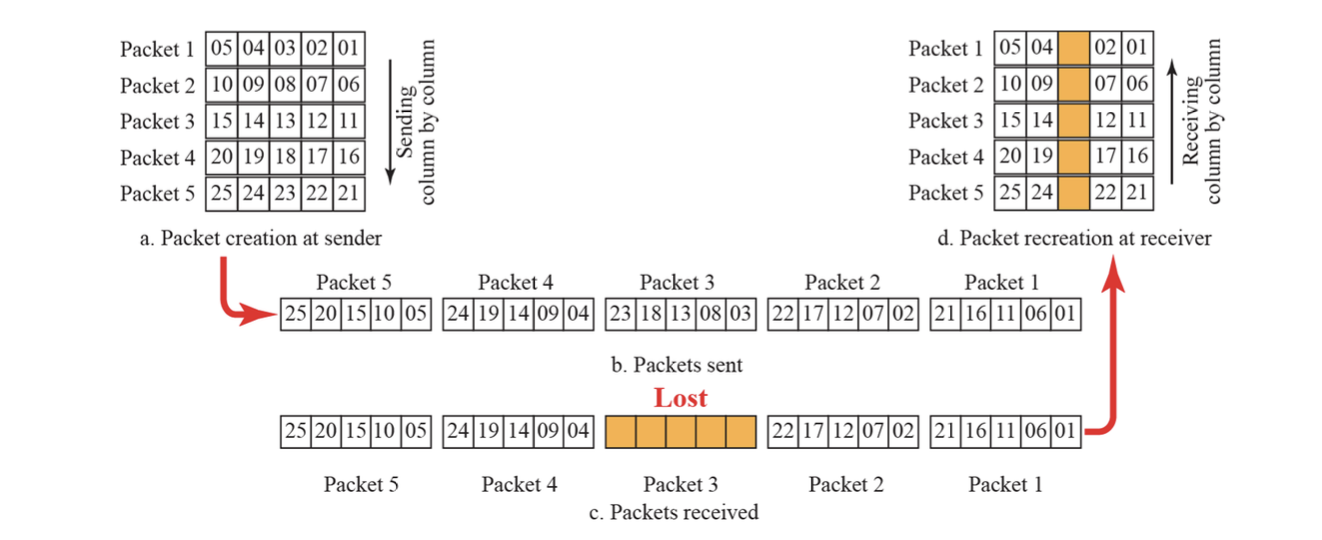
해밍 거리와 인터리빙의 결합

FEC는 단일 기법이 아니라 복합적으로 사용될 수 있다.

• 먼저, 각 n비트 패킷을 생성하면서 t비트 오류를 수정할 수 있는 해밍 거리를 확보한다.
• 그런 다음, 여러 패킷을 행(Row) 단위로 배열한 후 열(Column) 단위로 전송한다.(interleaving)
• 이 구조를 사용하면, burst error가 발생해도 각 행으로 분산되기 때문에 최대 m x t 비트까지 수정이 가능하다.

실시간 음성 코덱 등에서 종종 이 방식이 사용된다.

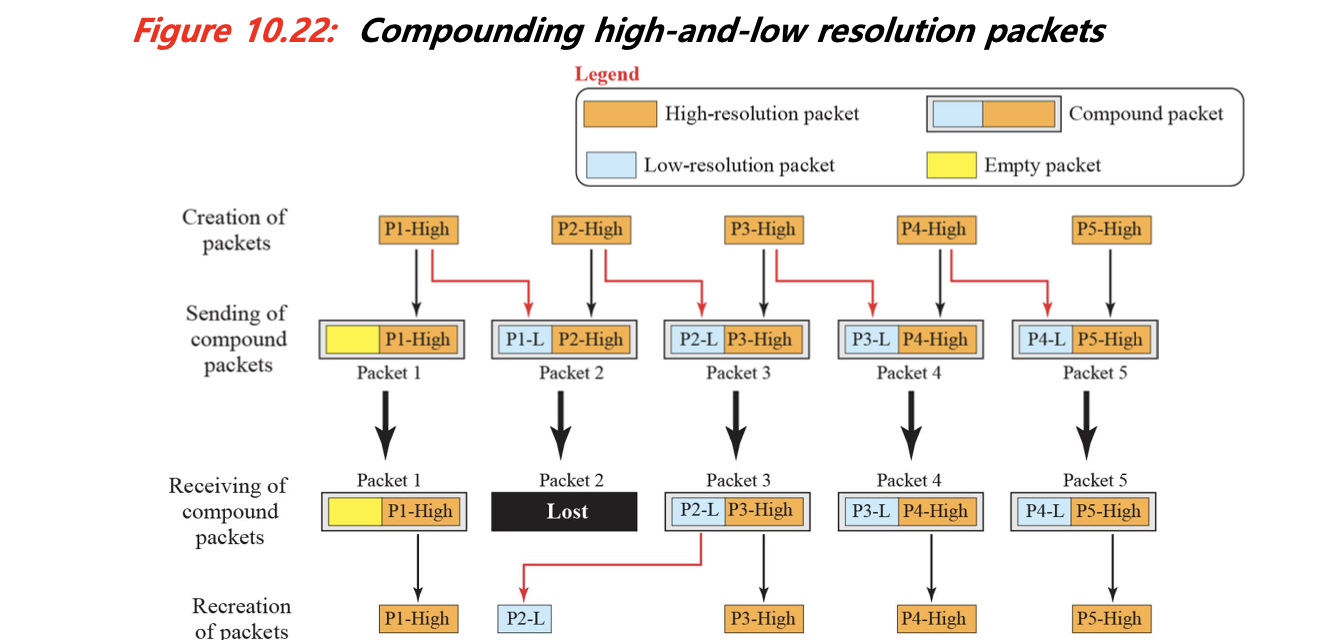
고해상도 - 저해상도 복합 전송 (Compounding)

가장 흥미로운 방식 중 하나는 데이터 품질을 조절해서 중복을 구성하는 것이다.

• 예를 들어, 5개의 고해상도(High-Res) 패킷에서 4개의 저해상도(Low-Res) 복사본을 만들어 중복으로 함께 전송한다.
• 수신자는 고해상도 패킷이 손실되더라도, 저해상도 복사본을 기반으로 일부분 복원할 수 있다.

이 방식은 스트리밍 영상처럼 “전부 정확하진 않아도 되지만, 일정 수준의 복구가 중요한” 상황에서 특히 유용하다.