[CS:APP] Chap2 A Representing and Manipulating Information(1)-Information Storage

10 minute read

현대 컴퓨터는 0과 1로 표현된 이진 신호를 이용해 정보를 저장하고 처리한다. 일반적으로 사람들에게는 10진법이 더 친숙할 수 있으나, 컴퓨터 설계에서는 이진법이 더 효율적으로 작동한다. 이진법은 유한 집합의 원소를 표현할 수 있으며, 숫자를 표현하는 방식에는 세 가지 중요한 방법이 있다. 첫 번째는 Unsigned Encodings으로, 0 이상의 숫자를 표현한다. 두 번째는 Two’s Complement Encodings으로, 음수와 양수 모두를 표현할 수 있다. 세 번째는 Floating-Point Encodings으로, 실수를 표현하는 데 사용된다.

컴퓨터는 제한된 비트 수로 숫자를 인코딩하며, 이는 오버플로우를 방지하기 위한 것이다. 예를 들어, 32비트 int 자료형을 사용하는 컴퓨터에서 200 * 300 * 400 * 500을 계산하면 -884,901,888이라는 값이 도출된다. 해당 계산에서는 교환 법칙과 결합 법칙이 성립하지만, 양수의 곱 결과가 음수로 나타나는 등 예상과 다른 결과가 나타날 수 있다. 그러나 컴퓨터가 생성한 결과는 일관성을 가지고 있다.

부동소수점 연산은 정수 연산과는 전혀 다른 수학적 특성을 가진다. 양수의 곱은 항상 양수를 반환하지만, 오버플로우가 발생하면 +무한대(∞)를 반환한다. 또한, 부동소수점 연산은 유한 정밀성(finite precision) 때문에 결합 법칙이 성립하지 않는다. 예를 들어, (3.14 + 1e20) - 1e20은 0.0을 반환하지만, 3.14 + (1e20 - 1e20)은 3.14를 반환한다. 이처럼 정수와 부동소수점 연산은 서로 다른 수학적 속성을 가지며, 유한성을 다루는 방식에 따라 차이를 보인다. 정수 연산은 비교적 작은 범위의 값을 인코딩하지만 정확한 값을 반환하며, 부동소수점 연산은 넓은 범위의 값을 인코딩할 수 있지만 대략적인 값을 반환한다.

컴퓨터는 숫자 값을 인코딩하기 위해 다양한 이진 표현 방식을 사용하며, 이는 값의 범위와 산술 연산의 특성을 이해하는 데 매우 중요하다. 이러한 이해는 이식성 있는 프로그램을 작성하고 보안 취약점을 방지하는 데 필요한 기초가 된다. 컴퓨터 산술의 미묘한 특성으로 인해 보안 취약점이 발생할 수 있으며, 해커들은 이러한 취약점을 악용하려고 한다. 따라서 프로그래머는 프로그램이 예상치 못한 방식으로 작동하지 않도록 깊이 이해하고 신중하게 작성해야 한다.

비트 수준의 표현을 직접 조작하여 산술 연산을 수행하는 방법은 중요한 기술이며, 이는 컴파일러가 생성하는 기계 수준 코드를 이해하고 최적화하는 데 필수적이다. 숫자 표현과 산술 연산의 특성을 깊이 이해하고 이를 바탕으로 보안에 강하며 효율적인 프로그램을 작성하는 것은 프로그래머의 중요한 역할이다.

2.1 Information Storage

메모리에서 개별 비트에 접근하기보다는, 대부분의 컴퓨터는 8비트 단위, 즉 바이트(byte)를 메모리에 가장 작은 주소 지정 가능 단위로 사용한다. 메모리의 모든 바이트는 고유한 번호(주소)로 식별되며, 이러한 주소의 집합은 가상 주소 공간(virtual address space)이라고 불린다. 가상주소 공간은 기계 수준 프로그램에서 제공되는 개념적 이미지일 뿐이며, 실제 구현은 DRAM, 플래시 메모리, 디스크 저장소, 특수 하드웨어, 운영 체제의 소프트웨어의 조합을 통해 프로그램에 단일 바이트 처럼 보이도록 구성된다.

가상 주소 공간 내에서, 메모리는 프로그램 데이터, 명령어, 제어 정보와 같은 다양한 프로그램 객체를 저장하기 위해 더 작은 단위로 분할된다. 이러한 메모리 공간의 분할과 관리는 컴파일러와 런타임 시스템에 의해 수행된다. 예를 들어, C언어에서 포인터 값은 특정 데이터 유형(정수, 구조체, 기타 프로그램 객체 등)의 첫 번째 바이트의 가상 주소를 나타낸다.(포인터는 데이터가 시작하는 위치, 즉 첫 번째 바이트의 주소를 기리킴을 의미)

C컴파일러는 포인터마다 데이터 타입 정보(type information)를 연결하여, 포인터가 지정하는 위치에 저장된 값의 타입에 따라 적절한 기계 수준 코드를 생성한다. 하지만 실제로 생성된 기계 수준 프로그램은 데이터 타입에 대한 정보를 유지하지 않는다. 프로그램은 단순히 바이트 블록으로 구성된 객체와 바이트 시퀀스로 이루어진 명령어로 처리된다.

2.1.1 Hexadecimal Notation(16진수 표기법)

1바이트(byte)는 8비트(bit)로 구성되며, 값의 범위는 다음과 같다.
- 이진수(Binary) : 00000000 ~ 11111111
- 십진수(Decimal) : 0~255
- 16진수(Hexadecimal) : 00 ~ FF
이진수는 표현이 너무 장황하고, 십진수는 비트 패턴과의 변환이 번거롭기 때문에, 이를 해결하기 위해 16진수(hex)를 사용한다.

16진수의 장점

이진수와 간단히 변환이 가능하다.
이진수의 장황함을 줄이고, 십진수의 변환 복잡성을 해결한다.

C언어에서의 16진수 표기

0x or 0X로 시작
ex. 0xAB691 0Xab691 0xAb691 모두 동일하다.(대소문자 상관X)

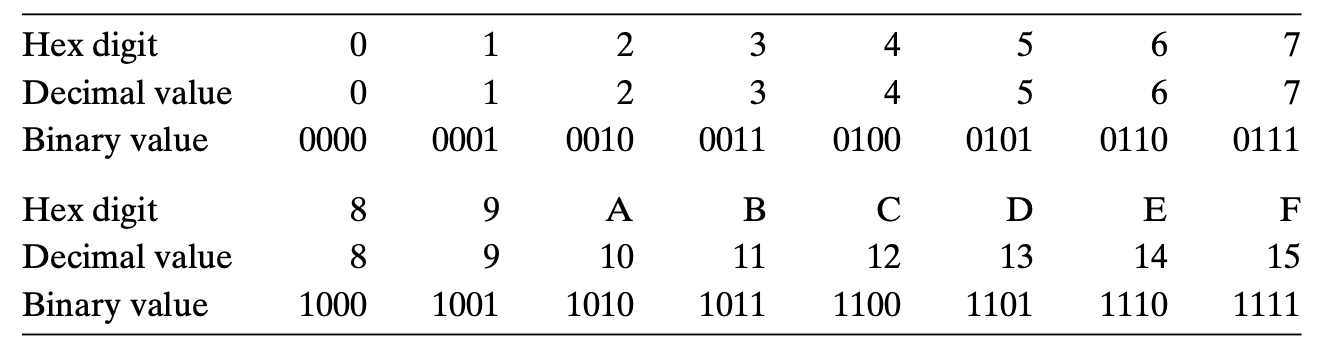
Alt text

16진수 2진수 변환

16진수 한 자리(hex digit)는 4개의 2진수 자리(bit)로 변환된다. 즉, 16진수의 각 자리를 4비트 이진수로 확장하면 된다.

Alt text

2진수 16진수 변환

2진수는 4비트씩 나누어 각 그룹을 16진수 숫자로 변환한다. 4비트로 나눌 때에는 오른쪽 부터 나누고, 가장 왼쪽의 비트 개수가 4개가 아니라면 0을 추가하여 4비트를 채워준다.

Alt text

만약 X(10진수 X)의 값이 2의 거듭제곱 꼴이라면, x = 2^n n을 4로 나눈 몫이 16진수의 0의 개수, 2의 “나머지”제곱이 16진수 가장 앞에 숫자가 된다.
- x=2^11 //n=11
- 11 = 3 + 4 x 2 이므로
- 16진수 표기 : 0x800 (가장 앞 숫자 8은 2^3, 0의 개수는 2개)

10진수 16진수 변환

마찬가지로 10진수 값을 16으로 나눈 몫과 나머지로 표현 할 수 있다.

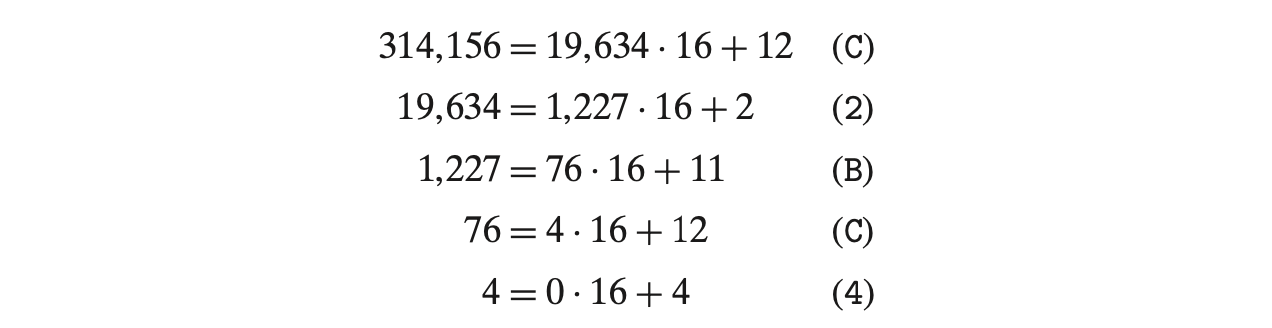
Alt text

314156의 hex 값은 : 0x4CB2C

16진수 10진수 변환

16진수 각 자리 숫자를 16의 적절한 거듭제곱으로 곱한 값을 모두 더하면 된다.
0xA7 의 경우 16^1 x 10(=A) + 16^0 x 7 = 167

16진수의 덧셈

0x605c + 0x5 = 0x6061 // 5 + c -> 16(캐리 발생) + 1
0x605c - 0x20 = 0x603c
0x605c + 32 = 0x607c
0x60fa - 0x605c = 0x9e

2.1.2 Data Sizes

컴퓨터의 워드 크기(word size)는 포인터 데이터의 명목 크기를 나타낸다. 가장 주소는 워드 크기로 인코딩되며, 워드 크기에 따라 가상 주소 공간의 최대 크기가 결정된다. 워드 크기가 w이면, 가상 주소 공간은 0부터 2^w-1 까지의 범위를 가지며, 이는 프로그램이 최대 2^w 바이트를 접근할 수 있음을 의미한다. 32비트 시스템은 최대 4GB의 주소 공간을 가지며, 64비트 시스템은 최대 16EB의 주소 공간을 갖는다.(워드는 CPU가 한번에 처리할 수 있는 data 크기를 의미하며, 32비트 시스템은 워드 크기가 32비트임을 의미한다.)

대부분의 64비트 컴퓨터는 32비트 프로그램을 실행 가능하며(하위 호환성 제공), 반대는 불가능하다.

C 언어의 데이터 타입 크기는 프로그램이 컴파일되는 환경에 따라 다르며, 아래 표는 각각의 일반적인 크기를 비교하기 위해 나타내고 있다.

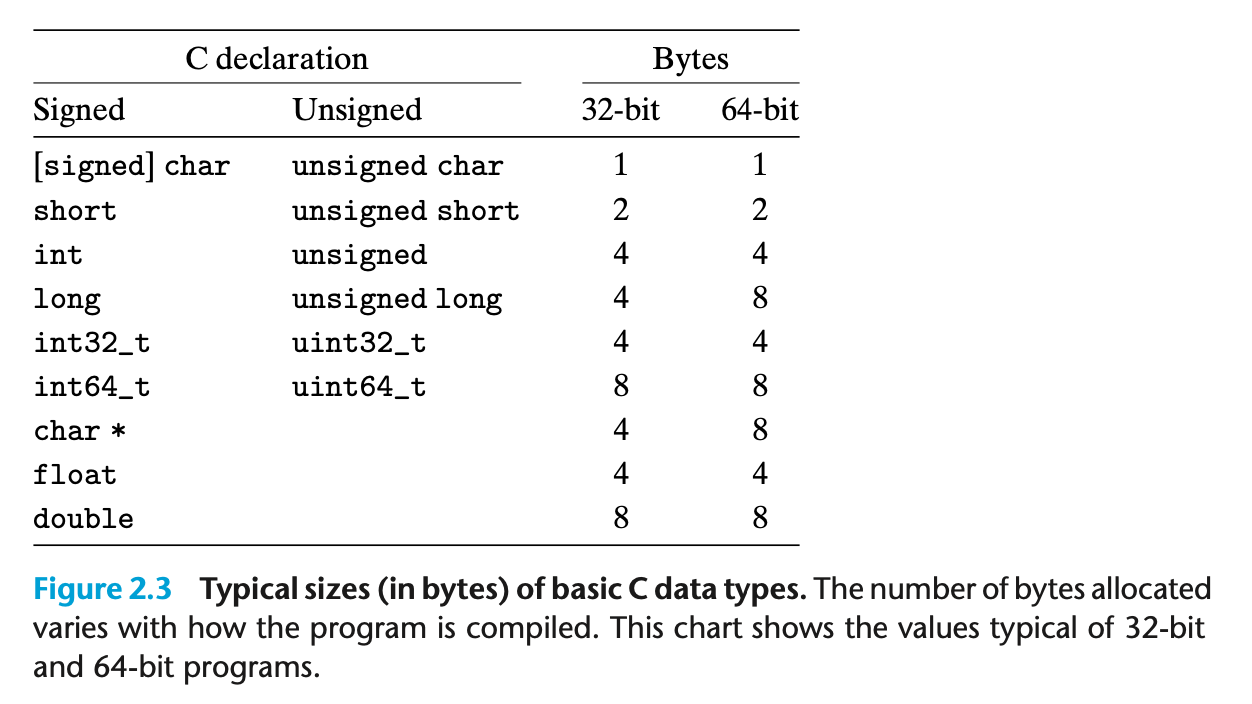
Alt text

컴파일러 환경에 따라 데이터 타입이 달라지는 문제를 해결하기 위해 ISO C99는 고정 크기 데이터 타입을 도입하였다.

- int32_t : 정확히 4바이트
- int64_t : 정확히 8바이트

이를 사용하면 데이터 표현을 세밀하게 제어가 가능하다.

대부분의 데이터 타입은 기본적으로 signed value(부호가 있는 값)으로 인코딩한다. 부호가 없는 값으로 처리를 하려면 Unsigned 키워드를 명시해줘야한다. 하지만 예외로 char가 있다. char는 C에서 부호의 존재를 보장하지않기 때문에 명시적 선언을 해주는 것이 안전하다.(보통 크게 중요하지않다.)

대부분 두 가지 부동소수점 형식을 지원한다.

- float(단정밀도, single precision) : 4bytes
- double(배정밀도, double precision) : 8bytes

포인터는 프로그램의 전체 워드 크기를 사용한다.

- 32비트 시스템 : 4bytes
- 64비트 시스템 : 8bytes

C 표준은 다양한 데이터 타입의 숫자 범위에 대해서 상한을 설정해놓지 않았다.(고정 크기 제외) 이로 인해 다음과 같은 문제가 발생한다. 보통 32비트 체제에 맞춰 설계되었기 때문에 64비트 체제에서 버그가 발생한다. 예를 들어 과거에는 많은 프로그래머들이 int 타입으로 선언된 객체가 포인터를 저장하는 데 사용할 수 있다고 가정했다. 이는 대부분의 32비트 프로그램에서는 문제없이 작동하지만, 64비트 프로그램에서는 문제를 일으킨다.(64비트 환경에서는 포인터 크기가 더 크기 때문에, int 타입으로 이를 저장하려고 하면 상위 4바이트가 잘려나가면서 오류가 발생한다.) 즉, 64비트 환경에서는 포인터와 데이터 타입 크기를 명확히 구분하는 것이 중요하다.

즉, C 프로그래밍에서 워드 크기, 데이터 타입 크기, 포인터 처리 등은 하드웨어와 컴파일러 차이에 영향을 받는다. 이를 고려해 이식성이 높은 프로그램을 작성하려면 고정 크기 데이터 타입 사용, 포인터 크기와 데이터 타입 크기를 혼동하지 말 것, 데이터 타입 선언 시 일관성을 유지할 것 세 가지를 지키는 것이 좋다. (데이터 타입 크기에 의존하지 않도록 설계하고 고정 크기 데이터 타입 사용을 권장한다.)

2.1.3 Adressing and Byte Ordering

Adressing and Storage of Multi-Byte Objects

주소 할당
- 다중 바이트 객체의 주소는 해당 바이트 중 가장 작은 주소로 설정
- ex. int x 가 주소 0x100에 위치하고, 32비트라면 바이트는 0x100, 0x101, 0x102, 0x103에 저장됨
바이트 저장 순서
- Little-endian : 가장 낮은 바이트부터 저장
- Big-endian : 가장 높은 바이트부터 저장
- ex. x=0x01234567 일때,
  - Big-endian : 0x100 = 0x01, 0x103 = 0x67
  - Little-endian : 0x100 = 0x67, 0x103 = 0x01

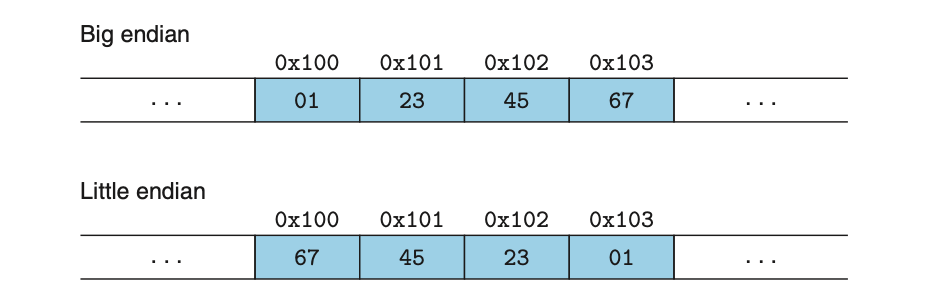
Byte Ordering Conventions

Little-endian
- 대부분의 Intel 호환 시스템에서 사용
- 데이터의 최하위 바이트부터 메모리에 저장
Big-endian
- IBM 및 Oracle 기반 시스템에서 주로 사용
- 데이터의 최상위 바이트부터 메모리에 저장
Bi-endian
- 일부 현대 프로세서는 little-endian과 big-endian 중 선택 가능
- ex. ARM 프로세서는 하드웨어적으로 양쪽 지원하나, Android와 iOS는 Little-endian 사용

Byte Ordering의 기술적 중요성

네트워크 통신
- 서로 다른 바이트 순서를 사용하는 시스템 간 통신 시, 데이터가 올바르게 해석되지 않을 수 있음.
- 해결책
  - 네트워크 표준으로 변환 후 전송
  - 수신 시 내부 표현으로 변환
바이트 시퀀스 분석
- Little-endian 시스템에서 생성된 기계 코드
  - 바이트가 역순으로 나타남
  - ex. 43 0b 20 00 -> 00 20 0b 43 (값 0x200b43)
C 프로그래밍에서 타입 시스템 우회
- 캐스팅(cast) 또는 유니언(union)을 사용해 객체를 다른 데이터 타입으로 참조 가능
- 이런 코드는 일반적으로 권장되지 않으나, 시스템 수준 프로그래밍에서는 필요할 수 있음
- 아래는 데이터 타입별 저장 형식과 시스템에 따른 차이 분석 코드

/*캐스팅(casting)을 사용하여 서로 다른 프로그램 객체의 바이트 표현을 액세스하고 출력하는 C코드
캐스팅 : 프로그래밍에서 데이터 타입을 변환하는 작업
*/
#include <stdio.h>

typedef unsigned char *byte_pointer;
//unsigned char 는 개별 바이트를 나타내는 데 사용되며, 각 바이트는 0-255 사이의 값을 가질 수 있다.
//byte_pointer는 메모리 주소를 바이트 단위로 참조할 수 있는 포인터

void show_bytes(byte_pointer start, size_t len){//메모리 주소(start) 와 길이(len) 입력
    int i;
    for(i=0; i<len; i++){
        printf("%.2x", start[i]);//각 바이트를 순차적으로 읽어 16진수로 출력한다.
    }
    printf("\n");
}

void show_int(int x){
    show_bytes((byte_pointer) &x, sizeof(int));//명시적 캐스팅
}

void show_float(float x){
    show_bytes((byte_pointer) &x, sizeof(float));
}

void show_pointer(void *x){ 
    show_bytes((byte_pointer) &x, sizeof(void *));
}
//각 타입의 데이터를 받아, 해당 데이터의 메모리 주소를 byte_pointer로 캐스팅 한 뒤, showbytes 출력

//sizeof의 사용 : 객체의 크기(바이트 수)를 동적으로 계산
// 이식성을 높이기 위해 sizeof를 사용하여 고정된 크기 대신 데이터 구조 크기를 자동 계산
int main(void){
    int num=4;

    show_int(num);//출력 결과 : 04000000
    //little endian은 LSB가 가장 낮은 메모리 주소에 저장되므로 04000000로 출력
    show_float(num);//출력결과 : 00008040
    //부호 : 0(양수)
    //지수 : 2^2 + 127 = 129 -> 0x81
    //가수 : 0
    show_pointer(num);// 출력 : 0400000000000000
    //포인터는 64비트 시스템에서 보통 8바이트로 표현됨
    //little endian 방식으로 메모리 표현
    //1바이트가 2자리의 16진수로 표현됨

    return 0;
}

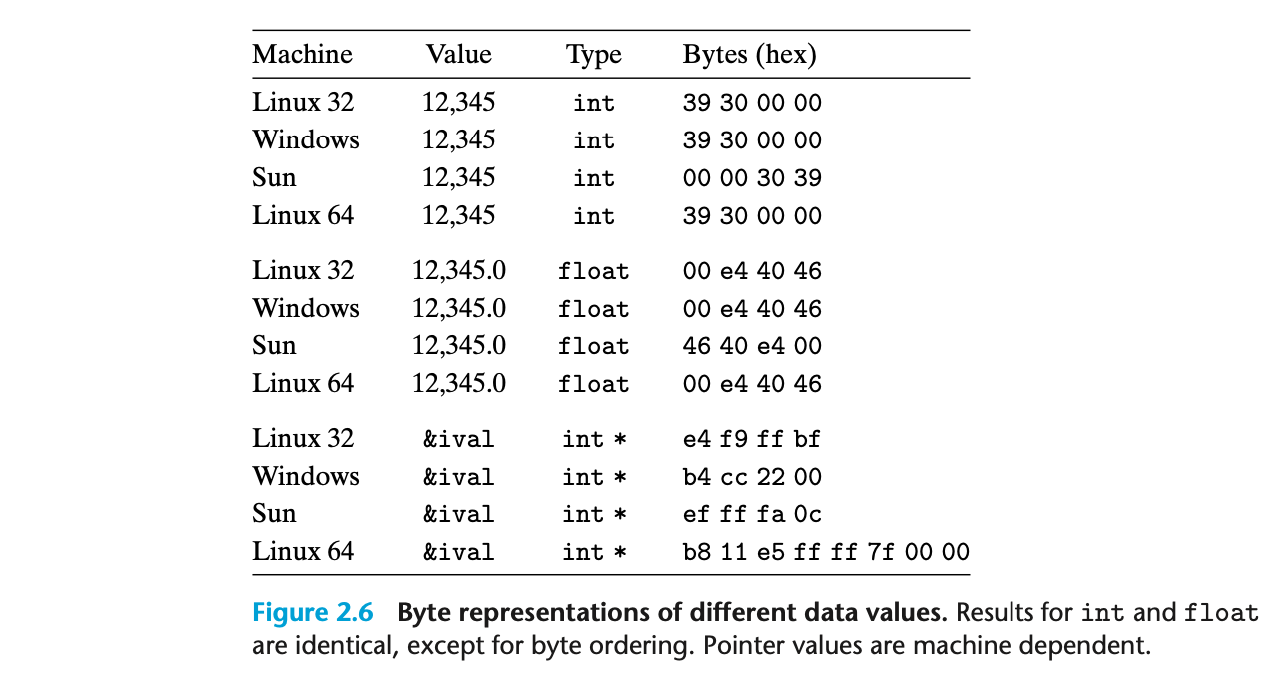
Alt text

int 와 float 값 비교
- 모든 시스템에서 값은 동일하나, endian(byte ordering)에 따라 순서가 다름
- Little-endian(Linux32, Windows, Linux64)
- Big-endian(Sun)
포인터(int * ) 값 비교
- 포인터 값은 운영체제와 프로세서 아키텍쳐에 따라 다르게 표현됨
  - Linux32, Windows, Sun : 4바이트 주소 사용
  - Linux64 : 8바이트 주소 사용

summary

Little-endian vs Big-endian
- 메모리에서 데이터 저장 순서는 시스템마다 다르며, 데이터 교환 및 분석에서 주의가 필요하다.
데이터 타입과 저장 형식
- int와 float은 동일한 값도 다른 저장 방식을 사용
포인터와 메모리 주소 크기
- 시스템에 따라 포인터 크기와 주소 표현 방식이 다름
이식성 문제(호환)
- 네트워크 데이터 교환 또는 다른 시스템에서 실행 시, 바이트 순서와 데이터 크기 차이로 문제가 발생할 수 있다.
- sizeof와 표준화된 데이터 변환을 통해 해결 가능하다.

Integer 와 Floating-Point 데이터의 바이트 패턴 비교

숫자값 12345의 저장 방식 비교
- int : 0x00003039
- float : 0x4640E400
- 동일한 값이라도, 정수와 부동소수점 데이터는 다른 인코딩 방식을 사용
2진수 변환 및 비교
- int : 00000000000000000011000000111001
- float : 01000110010000001110010000000000
- 두 데이터를 적절히 shift했을 때, 13개의 비트가 일치함(비트 패턴의 일부 유사성)
정수와 부동소수점 데이터는 다른 인코딩 방식을 사용하지만, 동일한 값을 표현할 때 일부 비트 패턴이 일치할 수 있다.

2.1.4 Representing Strings

C 문자열의 표현 방식

문자열은 문자 배열(char array)로 저장되며, 널 문자(null character, 0)로 종료된다.
각 문자는 ASCII 코드와 같은 표준 인코딩 방식으로 표현된다.

독립성

ASCII 코드로 표현된 텍스트 데이터는 endian(byte-ordering) 및 워드 크기(word size)와 무관하게 모든 시스템에서 동일한 결과를 얻는다.
즉, 텍스트 데이터는 바이너리 데이터보다 독립적이다.(이식성.portability가 높다)

2.1.5 Representing Code

int sum(int x, int y){
   return x+y;
}

머신 코드로 변환

각 플랫픔에서 컴파일된 머신 코드는 다음과 같은 바이트 시퀀스로 나타난다.

Alt text

바이트 표현의 차이

기계 아키텍쳐와 운영체제에 따라 명령어와 인코딩 방식이 다르다.
동일한 프로세서라도 운영체제가 다르면 코딩 방식이 호환되지 않을 수 있다.
결과적으로 바이너리 코드의 이식성(portability)은 매우 낮다.

기계 관점의 프로그램

기계는 프로그램을 바이트의 연속적인 시퀀스로 인식
소스 코드 정보는 저장되지 않으며, 디버깅을 위해 보조 테이블(auxiliary tables)이 일부 유지될 수 있다.

2.1.6 Introduction to Boolean Algerbra

Boolean Algebra의 정의

George Boole이 1850년대에 0과 1로 논리값(T/F)을 표현한 수학 체계를 제안
0은 false, 1은 true를 나타낸다.
컴퓨터 정보는 2진수로 저장하고 처리하기 때문에 Boolean Algebra는 핵심적인 역할을 한다.

Boolean 연산

NOT(~) : ~p는 p가 0일 때 1 , vice versa
AND(&) : p & q 는 p와 q가 둘 다 1일 때만 1
**OR( )** : p q 는 p 또는 q 중 하나라도 1일 때 1
XOR(^) : p ^ q 는 p 와 q 중 하나만 1일 떄 1

Bit Vectors 연산

비트 벡터 : 고정된 길이 w를 가진 0과 1의 문자열
ex. a=[0110], b=[1100]

Alt text

Bit Vectors를 활용한 집합 표현

비트 벡터는 유한 집합을 표현하는 데 유용하다.
- 비트 a[i] = 1 이면 원소가 i인 집합에 표현됨
- ex.
  - a = [01101001] : 집합 A = {0,3,5,6}
  - b = [01010101] : 집합 B = {0,2,4,6}
- 연산과 집합 연관성
  - a b : 집합의 합집합
  - a&b : 집합의 교집합
  - ~a : 집합의 여집합

2.1.7 Bit-Level Operations in C

C의 비트 연산 지원

C언어는 비트 단위 논리 연산을 지원한다.
**[ , &, ~, ^]** 이 연산자들은 정수형 데이터 타입에 적용이 가능하다.

Alt text

마스킹 연산(Masking Operations)

마스크(Mask) : 특정 비트를 선택하기 위해 사용하는 비트 패턴
0xFF(최하위 8비트가 1)
- x & 0xFF : x의 최하위 바이트만 남기고 나머지 바이트는 0으로 설정
- x ^ ~0xFF : x의 최하위 바이트만 남기고 나머지는 보수처리
- **x 0xFF** : 최하위 바이트를 1로 설정
모든 비트를 1로 설정하는 마스크 : ~0
- 데이터 표현 크기에 상관없이 모든 비트를 1로 설정
- 32비트 Int : 0xFFFFFFFF <- 크기가 고정된 표현은 이식성(portability)이 낮음

2.1.8 Logical Operations in C

C의 논리 연산자

논리 연산자는 비트 연산자와 혼동될 수 있으나 동작 방식이 다름
- ** (OR)**
- &&(AND)
- ! (NOT)

Alt text

논리 연산자는 첫 번째 인자만으로 결과가 결정되면 두 번째 인자를 평가하지 않는다
a && 5/a : a가 0이면 false (두 번재 인자는 평가되지 않는다.)->0으로 나누기 오류 방지
p && *p++ : p가 NULL(0)이면 첫 번째 인자가 false -> 두 번째 인자는 평가되지 않는다 NULL포인터 역참조 오류 방지

2.1.9 Shift Operations in C

Shift 연산의 정의

왼쪽 시프트( x « k )
- 비트를 K칸 왼쪽으로 이동한다.
- 가장 왼쪽 k개의 비트를 버리고, 오른쪽 끝을 0으로 채운다.
오른쪽 시프트( x » k)
- 비트를 k칸 오른쪽으로 이동
- 논리적 시프트(Logical Right Shift)
  - 왼쪽 끝을 0으로 채운다.
- 산술적 시프트(Arithmetic Right Shift)
  - 왼쪽 끝을 MSB(최상위 비트)로 채운다(부호 유지)

Alt text

주의점

이식성 문제 : C에서 signed 값의 오른쪽 시프트 방식이 시스템마다 다르므로, 코드를 작성할 때 주의해야한다.
Shift 연산 결과 : 결과는 2진수로 계산한 뒤, 16진수로 변환해 표현하는 것이 가장 명확하다.

Share on

Twitter Facebook LinkedIn

Yeontachi

[CS:APP] Chap2 A Representing and Manipulating Information(1)-Information Storage

2.1 Information Storage

2.1.1 Hexadecimal Notation(16진수 표기법)

2.1.2 Data Sizes

2.1.3 Adressing and Byte Ordering

2.1.4 Representing Strings

2.1.5 Representing Code

2.1.6 Introduction to Boolean Algerbra

2.1.7 Bit-Level Operations in C

2.1.8 Logical Operations in C

2.1.9 Shift Operations in C

Share on

You may also enjoy

[소프트웨어 공학] System modeling(2)

[컴퓨터 구조] 부동 소수점 (Floating Point)

[소프트웨어 공학] System modeling(1)

[OS] 파일 시스템 - File Systems