[CS:APP] Chap2 A Representing and Manipulating Information(2)-Integer Representation

2.2 Integer Representations

이 섹션은 정수를 표현하는 두 가지 비트 기반 방식 (Unsigned, Signed)을 소개하고, 비트 확장 및 축소가 값에 미치는 영향을 다룬다. 아래는 용어를 정리한 표이다.

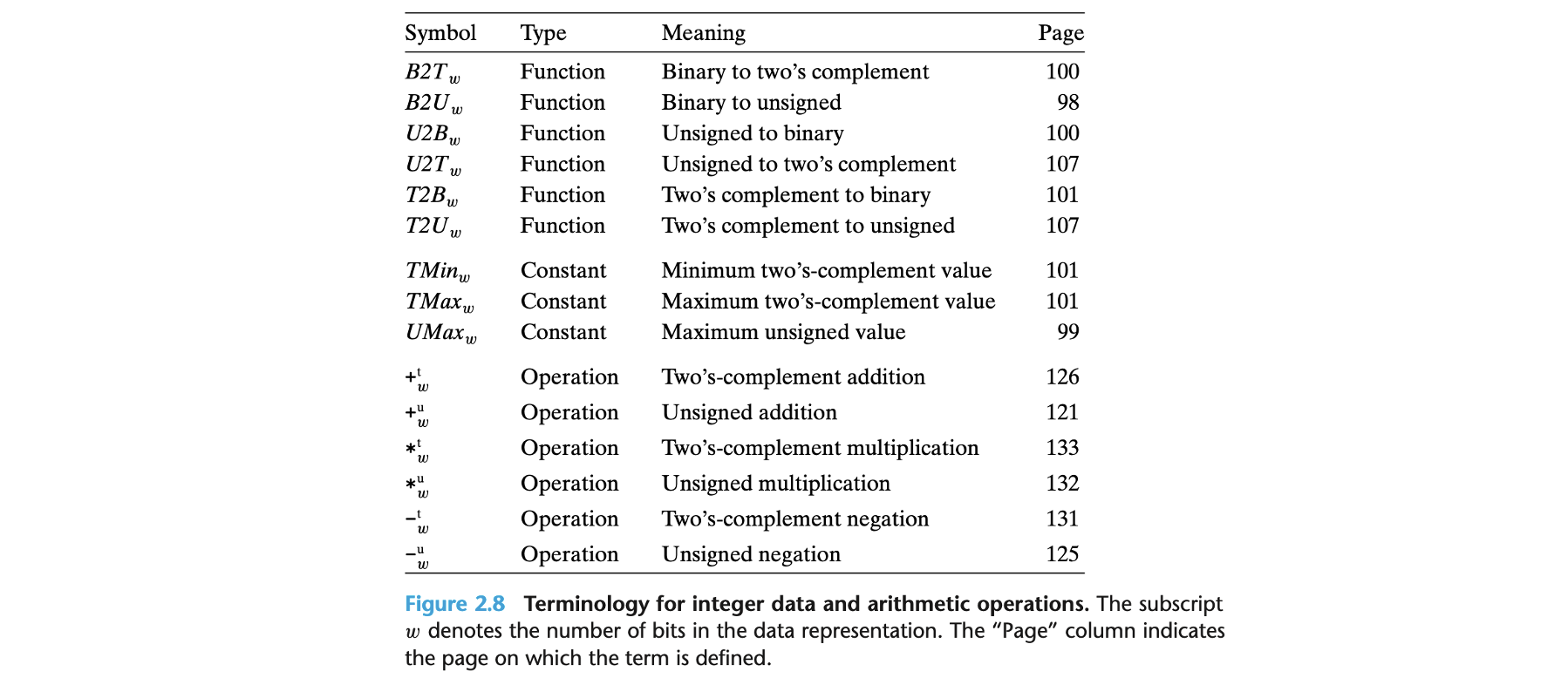
2.2.1 Integral Data Types

C언어는 다양한 정수형 데이터 타입을 지원하며, 각 데이터 타입은 특정한 크기와 범위를 가진다. 이 데이터 타입들은 char, short, int, long과 같은 키워드를 통해 크기를 지정할 수 있고, 부호 있는 값(signed)과 부호 없는 값(unsigned)을 표현할 수 있다. C 표준은 각 데이터 타입이 표현할 수 있는 최소한의 범위를 정의하며, 이는 모든 구현에서 반드시 충족되어야 한다. 표준에서 요구하는 범위는 양수와 음수의 범위가 대칭적이지만, 실제 구현에서는 음수 범위가 양수 범위보다 하나 더 크다(2의 보수 표현 방식에서 발생)

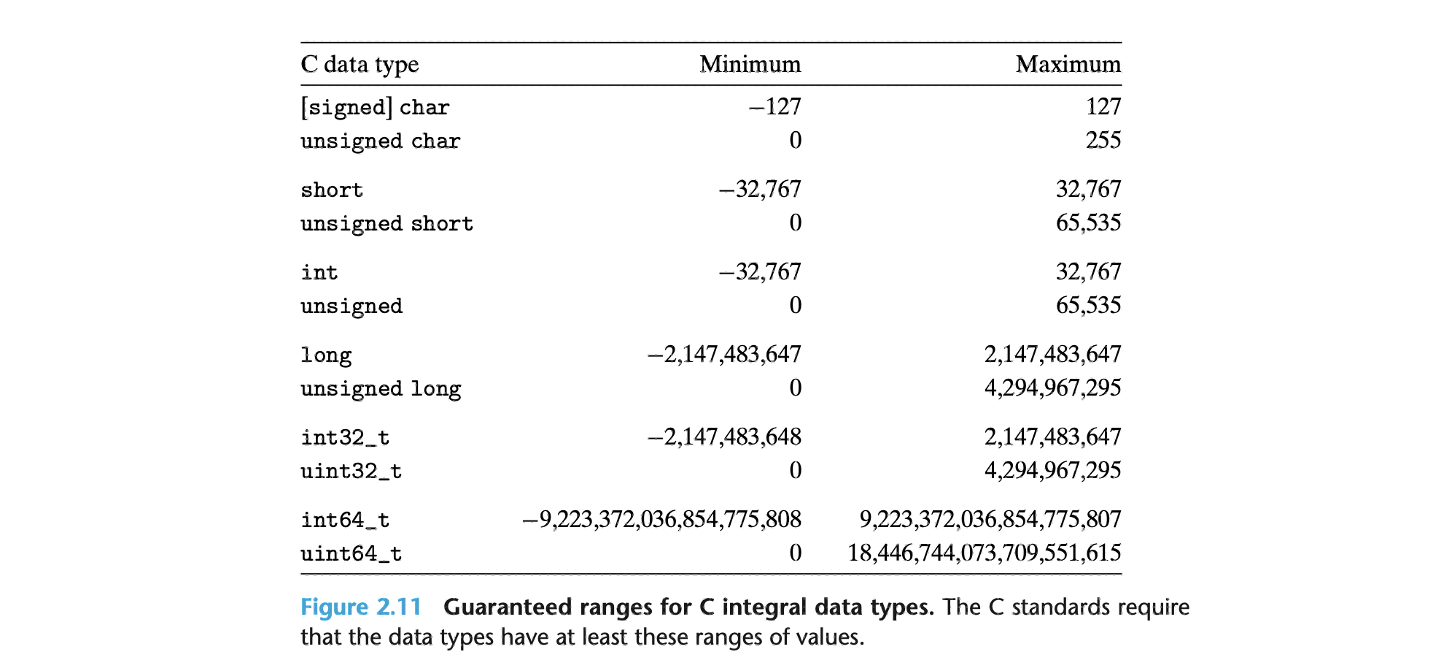
위 표는 C 표준에서 요구하는 범위이다. 즉, C 표준에서 명시적으로 규정한 데이터 타입의 최소 범위이다.

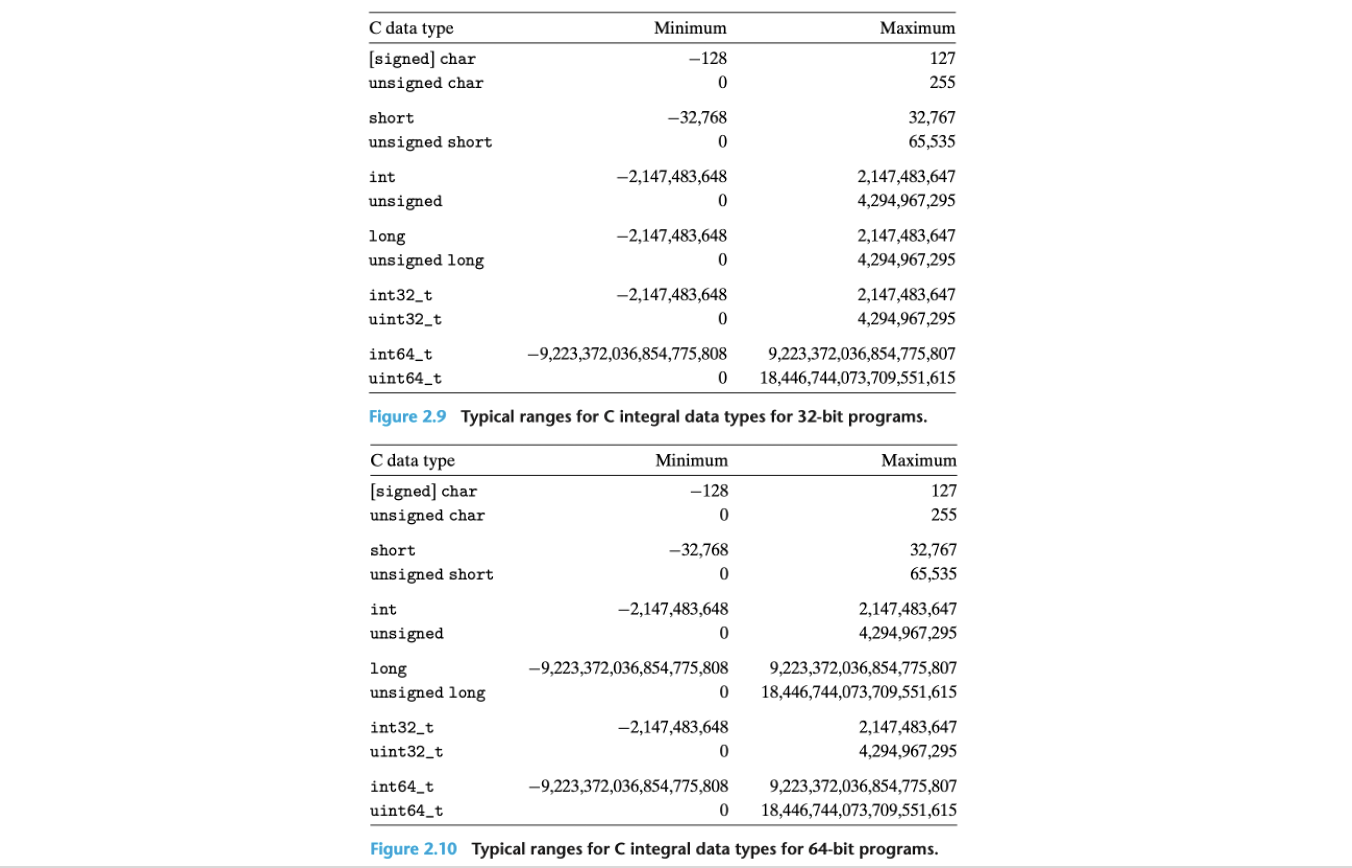
C 언어의 데이터 타입 크기와 값의 범위는 프로그램이 어느 환경에서(32비트 or 64비트) 실행되느냐에 따라 달라진다. 위에 표는 32비트와 64비트 환경에서의 일반적인 범위를 나타낸다. (일반적인 범위(typical range) : 특정 데이터 타입이 실제로 구현된 범위)

위 표에서 보여주는 일반적인 범위는 C표준에서 요구하는 최소 범위보다 크거나 같으며, 음수와 양수의 범위가 비대칭적인 특징을 갖는다.

데이터 타입 크기는 프로그램의 환경에 따라 달라질 수도 있다. 예를 들어, long 타입의 경우 32비트 환경에서는 4바이트로 제한되어 값의 범위가 좁지만, 64비트 환경에서는 8바이트로 구현되어 매우 넓은 값을 표현할 수 있다.

고정 크기 데이터 타입(int32_t, uint32_t…)은 정확히 정해진 크기와 값을 보장한다. 음수와 양수의 비대칭성이 유지되며, 데이터 타입의 크기에 따라 숫자의 표현 범위가 달라진다. 이러한 범위는 바이트 할당량에 의해 결정된다. (C 표준에서 요구하는 범위를 나타낸 표와 실제 구현된 범위를 나타낸 표를 비교해보면 고정 크기 데이터 타입은 최소,최대 크기가 비대칭성을 그대로 유지하는 것을 확인할 수 있다.)

실제 구현된 값의 범위가 대칭적이지 않은 이유는 2의 보수 표현 방식 때문이다. 음수를 표현할 때 부호 비트를 포함해 양수보다 하나 더 많은 값을 표현할 수 있으므로, 음수 범위가 더 넓어진다.

2.2.2 Unsigned Encodings

C 언어에서 정수를 표현하기 위해 비트를 사용하는 방식 중 하나는 부호 없는 정수(unsigned integer)를 표현하는 것이다. 이를 위해 비트 벡터(bit vector)라는 개념을 사용하며, 비트 벡터는 X=[x_w-1, x_w-2,…,x₀]와 같은 형식으로 표현된다. 여기서 w는 비트의 길이를 나타낸다. 각 비트는 0과 1의 값을 가지며 x_i = 1일 경우 해당 위치의 가중치가 2ⁱ가 숫자 값에 포함된다. 이렇게 비트 벡터를 부호 없는 정수로 변환하는 과정을 함수 B2U_w로 정의할 수 있다.

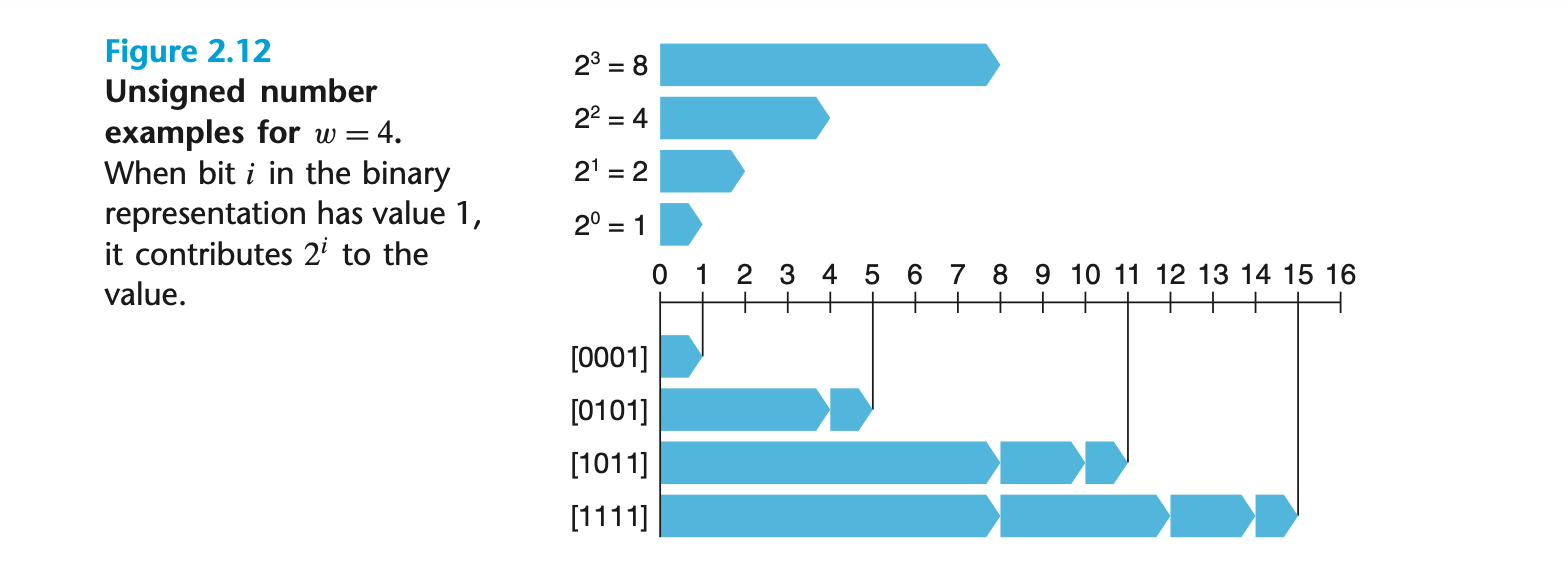
함수 B2U_w는 비트 벡터를 부호 없는 정수로 변환하며, 다음과 같은 수식으로 표현된다.

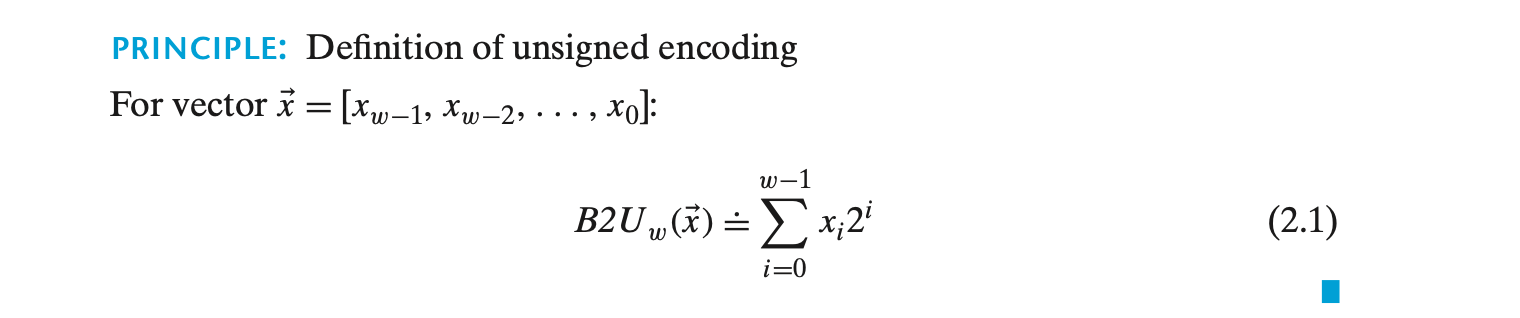
이 함수는 길이가 w인 비트 벡터를 0에서 2^w - 1 사이의 값으로 매핑한다. 예를 들어 4비트의 경우

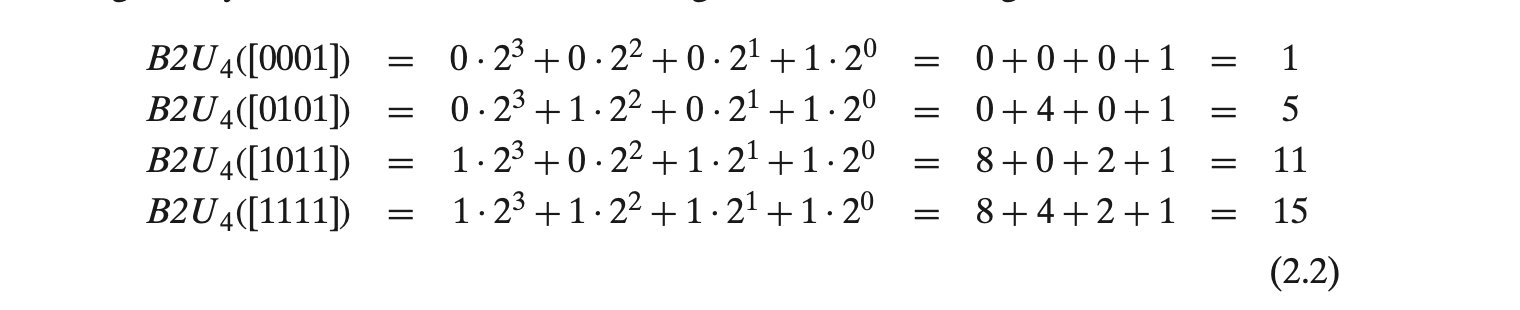
부호 없는 정수로 표현할 수 있는 값의 범위는 w-비트에 따라 달라진다. 최소값은 비트 벡터가 모두 0인 경우이며, 최대값은 모든 비트가 1인 경우로, 이를 2^w - 1로 계산할 수 있다.

B2U_w 함수는 고유성(Uniqueness)을 보장한다. 즉, 각 비트 벡터는 고유한 숫자 값에 매핑되며, 반대로 각 숫자 값도 고유한 비트 벡터에 매핑된다. 이러한 매핑은 전단사 함수(bijection)로 정의되며, B2U_w의 역함수 U2B_w를 통해 숫자에서 비트 벡터로 변환이 가능하다.

결론적으로 B2U_w 함수는 비트 벡터를 부호 없는 정수로 변환하는 데 사용되며, 최소값 0에서 최대값 2^w - 1 까지의 범위를 가진 숫자와 비트 벡터 간의 고유한 매핑을 제공한다.

2.2.3 Two’s-Complement Encodings

컴퓨터에서 정수를 표현하는 가장 일반적인 방법 중 하나는 2의 보수(Two’s Complement) 방식이다. 이 방식은 가장 높은 비트(MSB, most significant bit)를 음수 가중체를 가지는 부호 비트(sign bit)로 해석하여 음수와 양수를 모두 표현할 수 있다. 2의 보수 표현을 수학적으로 정의한 함수 B2T_w는 다음과 같이 정의된다.

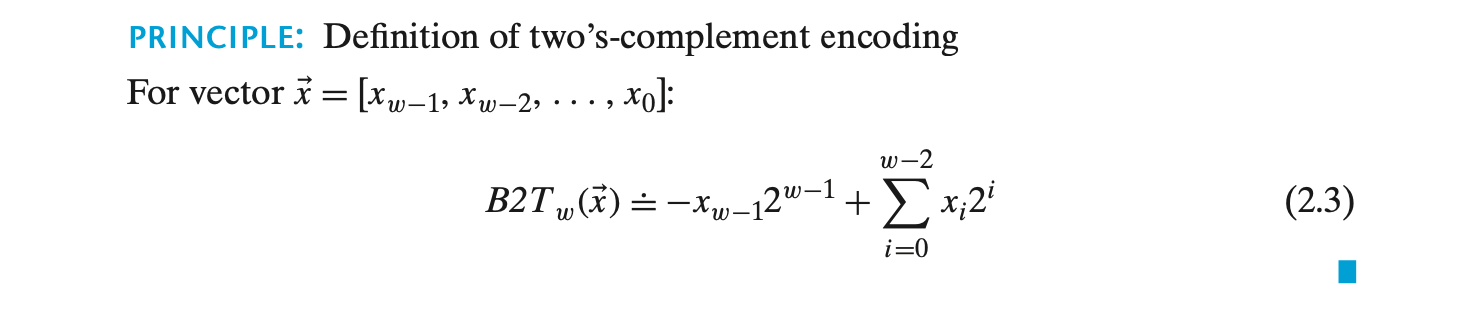
여기서 x_w-1은 부호 비트를 나타내며, 1일 경우 음수를, 0일 경우 양수나 0을 나타낸다. 이 정의는 비트 벡터를 음수와 양수로 매핑한다.

w-비트 숫자의 범위는 TMin_w = -2_w-1부터 TMax_w = -2_w-1 - 1이다.

이 방식에서 비트 벡터는 유일한 숫자 값에 매핑되며, 역함수 T2B_w를 통해 숫자를 비트 벡터로 변환할 수 있다. 이는 전단사 함수(bijection)로, 각 수자는 고유한 비트 벡터로 표현된다.

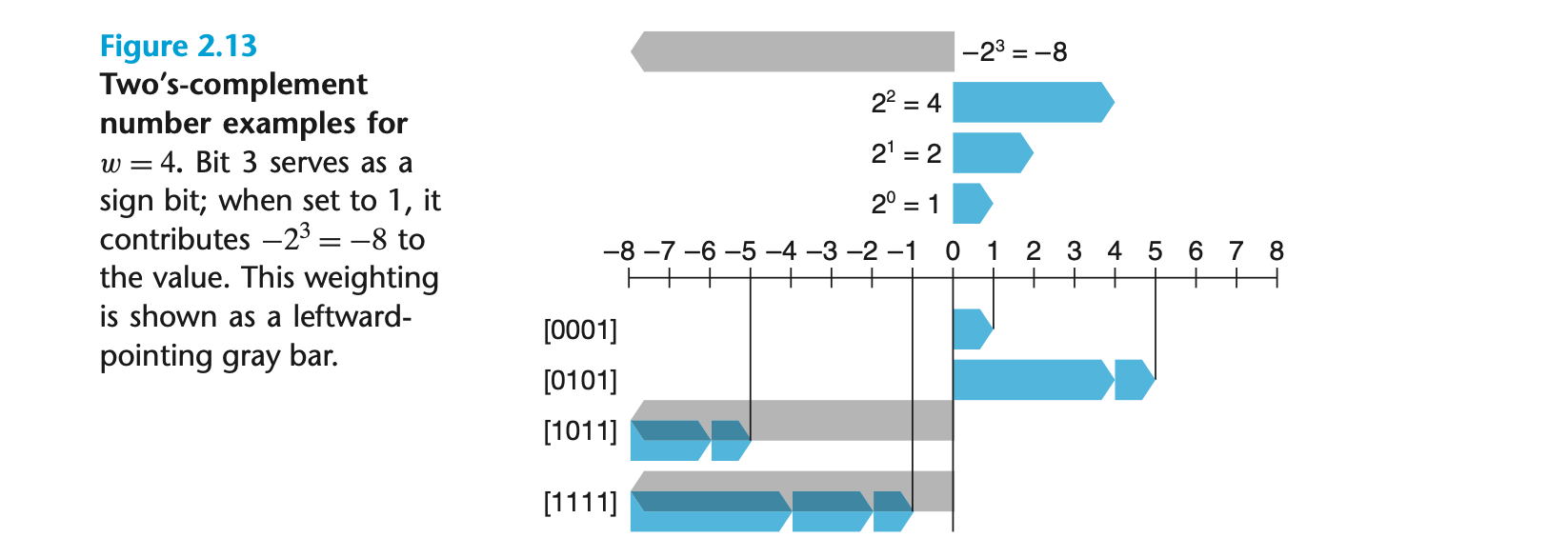
2의 보수 범위의 특징

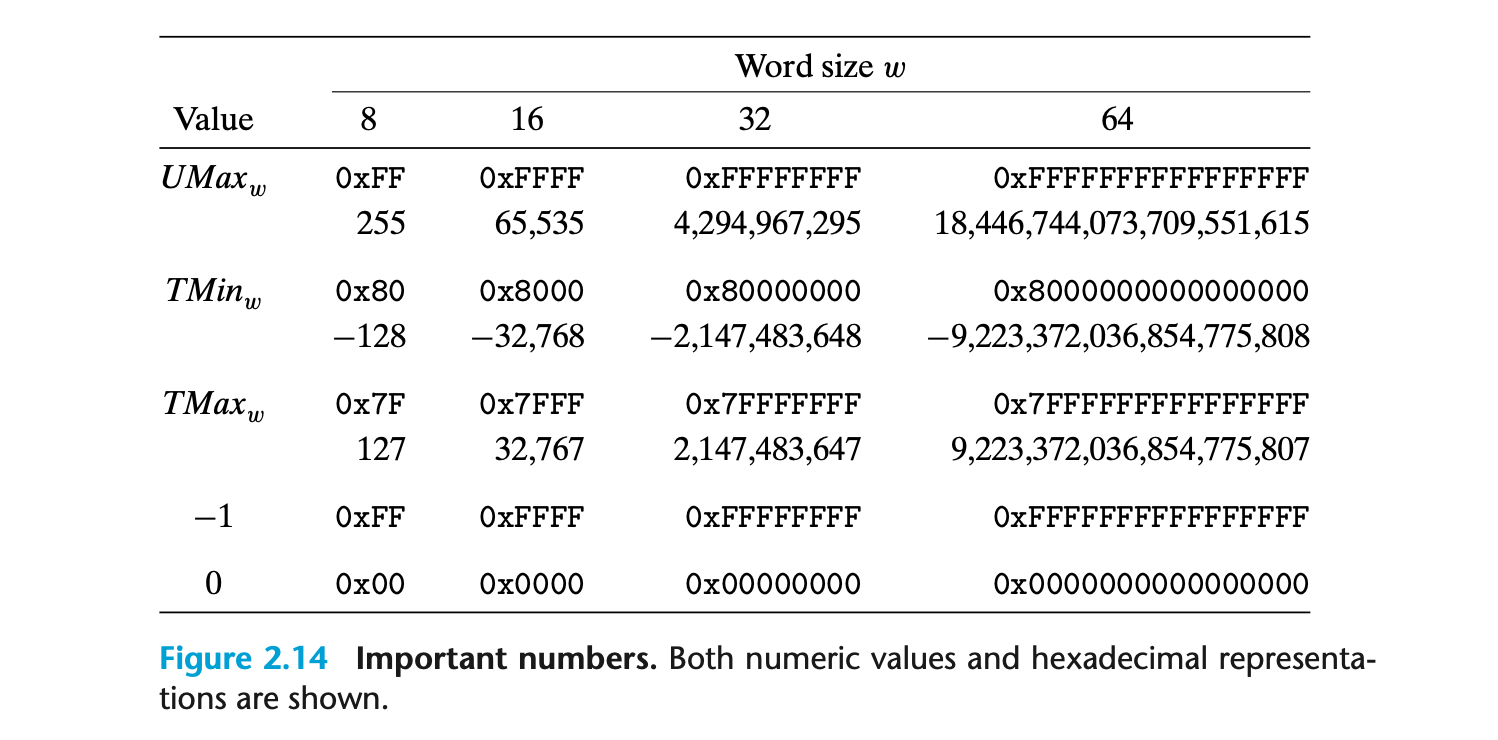
1. 비대칭적 범위
   • 0이 양수로 포함되기 때문에, 음수의 범위는 양수보다 하나 더 많다.

   • (

     TMin

     =

     TMax

     + 1).

2. 최대값과 최소값
   • 최대값 : TMax_w = -2_w-1 - 1
   • 최소값 : TMin_w = -2_w-1
3. 비트 패턴 비교
   • 2의 보수와 부호 없는 값의 비트 패턴은 동일하지만, 해석 방식이 다르다.
   • 예를 들어, 2의 보수에서 -1은 부호 없는 값의 최대값(UMax)과 동일한 비트 패턴을 가진다.

C 표준은 2의 보수 방식을 필수로 요구하지 않지만, 대부분의 시스템은 2의 보수를 사용한다. Java는 2의 보수를 필수로 요구하며, 데이터 타입의 범위와 표현 방식을 명확히 정의한다.

코드 예제

short x = 12345;
short mx = -x;

show_bytes((byte_pointer) &x, sizeof(short));
show_bytes((byte_pointer) &mx, sizeof(short));

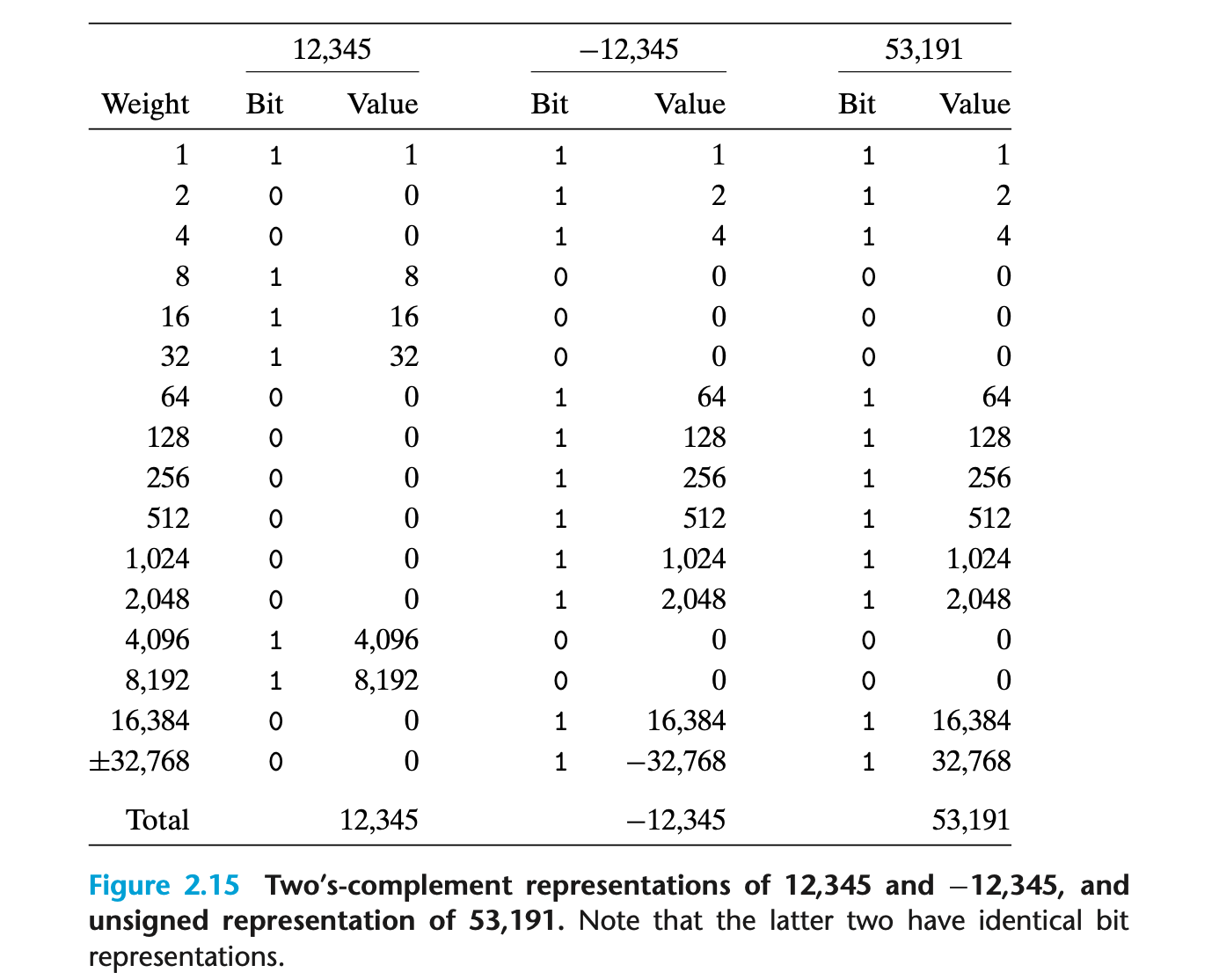
• x = 12345는 16진수로 0x3039, 이진수로 [0011000000111001]
• mx = -12345는 16진수로 0xCFC7, 이진수로 [1100111111000111]

2.2.4 Conversions between Signed and Unsigned

C언어에서는 부호 있는 정수(Signed)와 부호 없는 정수(Unsigned) 간의 캐스팅(Casting)이 가능하다. 캐스팅은 비트 패턴은 유지하되, 숫자 해석 방식을 변경한다. 이 변환은 비트 레벨 관점에서 이루어져, 숫자 값이 변할 수 있지만, 비트 패턴은 동일하다.

부호 있는 값에서 부호 없는 값으로 변환 (T2U)

부호 있는 값에서 부호 없는 값으로 변환 시, 음수는 부호 없는 양수로 변환된다.

 short int v = -12345;
 unsigned short uv = (unsigned short)v;
 printf("v = %d, uv = %u\n", v, uv);

출력 결과 : v = -12345, uv = 53191

T2U₁₆(-12345) = -12345 + 2¹⁶ = 53191

T2U 함수의 수학적 정의

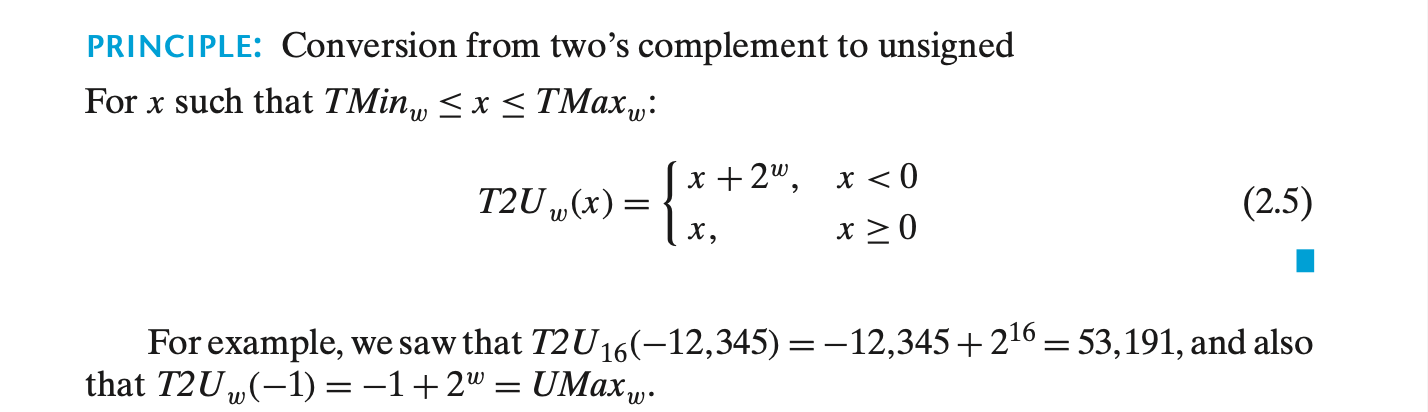
T2U₁₆(-12345) = -12345 + 2¹⁶ = 53191 T2U₃₂(-1) = -1 + 2³² = 4294967295

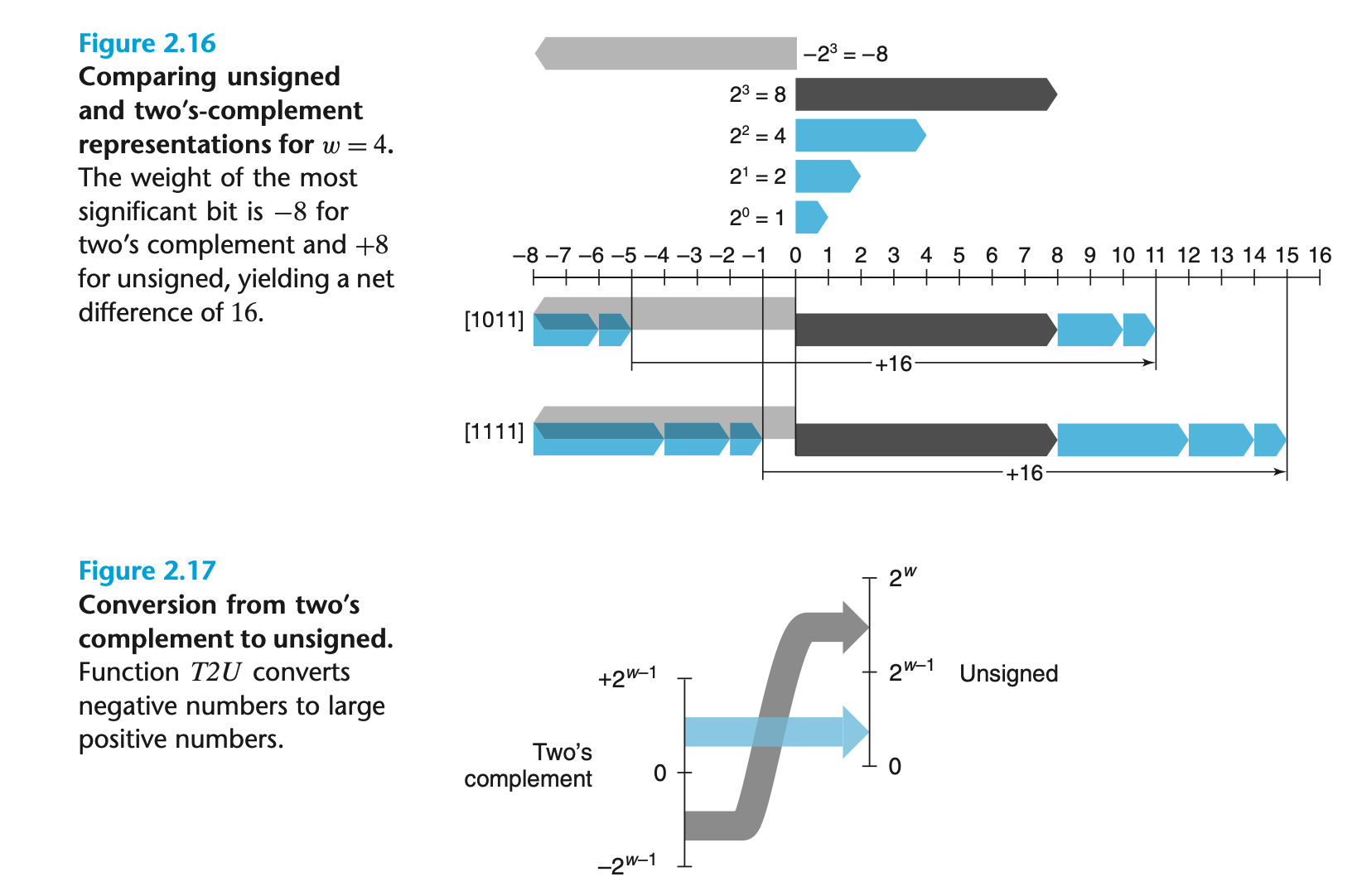
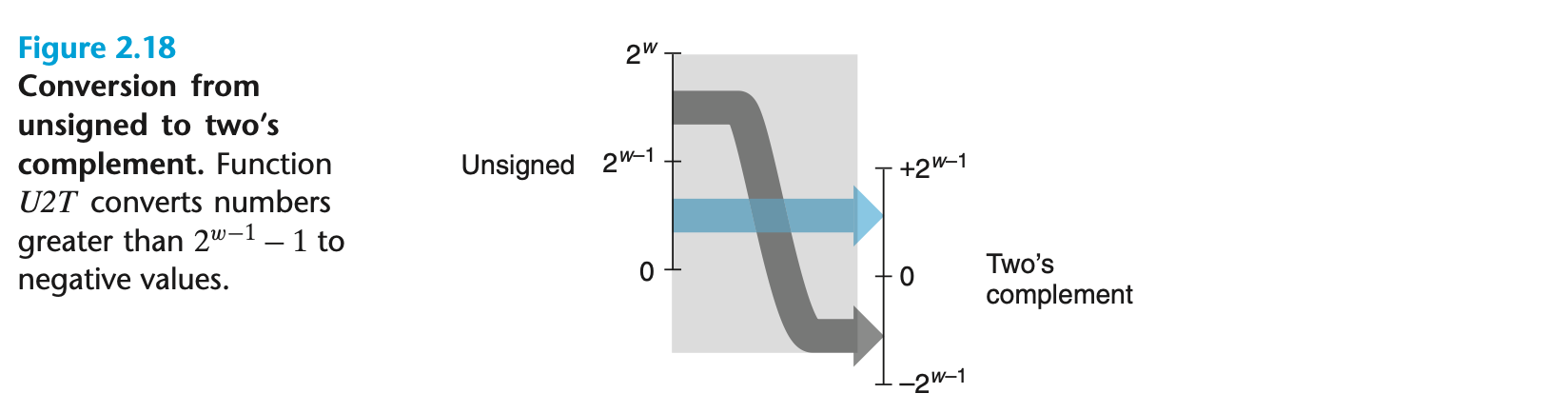
부호 없는 값에서 부호 있는 값으로 변환 (U2T)

부호 없는 값에서 부호 있는 값으로 변환 시, TMax보다 큰 값은 음수로 변환된다.

 unsigned u = 4294967295; /* UMax */
 int tu = (int)u;
 printf("u = %u, tu = %d\n", u, tu);

출력 결과 : u = 4294967295, tu = -1

U2T₃₂(4294967295) = 4294967295 + 2³² = -1

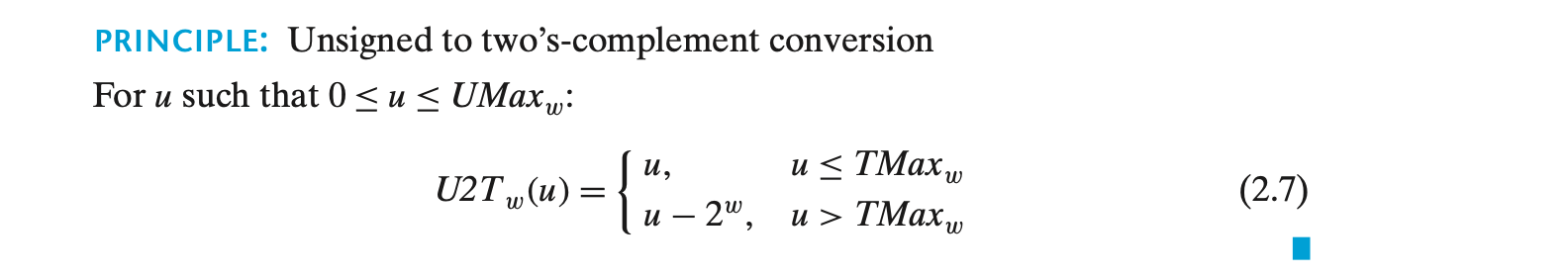
2.2.5 Signed versus Unsigned in C

C 언어는 모든 정수 데이터 타입에서 Signed,Unsigned 연산을 지원한다. C 표준은 부호 있는 숫자를 특정 방식으로 표현해야 한다고 명시하지 않지만, 거의 모든 시스템이 2의 보수(Two’s complement)표현을 사용한다. 기본적으로 숫자는 부호 있는 값으로 간주되며, 숫자 뒤에 U(u)를 추가하면 부호 없는 값이 된다.

값의 변환

1. 명시적 변환(Explicit Casting)

    int tx, ty;
    unsigned ux, uy;

    tx = (int) ux;   /* 부호 없는 값을 부호 있는 값으로 변환 */
    uy = (unsigned) ty; /* 부호 있는 값을 부호 없는 값으로 변환 */

1. 암묵적 변환(Implicit Casting)

    int tx, ty;
    unsigned ux, uy;

    tx = ux; /* 암묵적으로 부호 없는 값을 부호 있는 값으로 변환 */
    uy = ty; /* 암묵적으로 부호 있는 값을 부호 없는 값으로 변환 */

변환 과정에서 비트 패턴은 변경되지 않으며, 단순히 해석 방식만 달라진다.

printf를 사용한 출력

printf는 %d, %u, %x 형식을 사용해 부호 있는 정수, 부호 없는 정수, 16진수로 값을 출력한다. 그러나 printf는 변수의 타입 정보를 활용하지 않으므로, 부호 있는 값과 부호 없는 값을 서로 바꿔 출력할 수 있다.

 int x = -1;
 unsigned u = 2147483648; /* 2^31 */

 printf("x = %u = %d\n", x, x);
 printf("u = %u = %d\n", u, u);

출력 결과

• x = 4294967295 = -1 (-1의 비트 패턴은 UMax와 동일하다.)
• u = 2147483648 = -2147483648(2147483648 비트 패턴은 -2147483648(TMin)와 동일하다.)

값의 비교

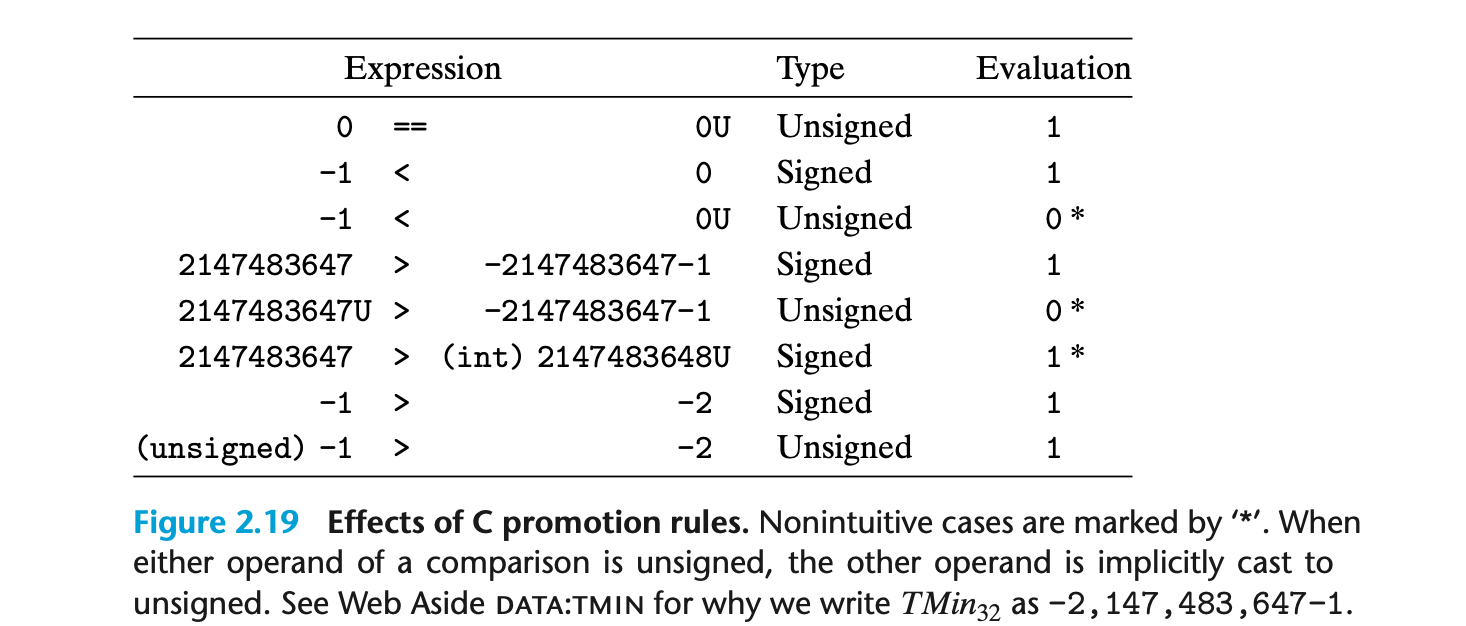
C에서는 부호 있는 값과 부호 없는 값이 섞인 표현식에서 암묵적으로 부호 있는 값이 부호 없는 값으로 변환된다. 연산은 모두 부호 없는 값으로 처리되며, 이로 인해 비교 연산자에서 비직관적인 결과가 발생할 수 있어 주의가 필요하다.

2.2.6 Expanding the Bit Representation of a Number

C 언어에서는 데이터 타입의 크기를 변경하면서 동일한 숫자 값을 유지해야 하는 경우가 자주 발생한다. 작은 타입에서 큰 타입으로의 변환은 항상 가능하며, 이 과정에서 값을 유지하기 위해 Zero Extension과 Sign Extension이라는 두 가지 확장 방식을 사용한다.

Zero Extension(부호 없는 값의 확장)

부호 없는 값을 더 큰 데이터 타입으로 변환할 때 사용한다.

• 새로운 비트 위치는 모두 0으로 채워진다.
• 이는 숫자 값에 영향을 미치지 않는다.
• B2U_w(u) = B2U_w’(u’)
• w’ > w, u’은 기존 벡터 u의 앞부분에 0이 추가된 형태이다.

Sign Extension(부호 있는 값의 확장)

2의 보수(부호 있는 값)를 더 큰 데이터 타입으로 변환할 때 사용한다.

• 가장 높은 비트(MSB, 부호 비트)를 복사하여 새로운 비트 위치를 채운다.
• 부호 비트가 1이면 음수, 0이면 양수 값이 유지된다.
• B2T_w(x) = B2T_w’(x’)
• 여기서 w’ > w, x’은 기존 비트 벡터 x의 앞부분에 부호 비트 x_w-1가 추가된 형태이다.

예제 코드

short sx = -12345; /* -12345 */
unsigned short usx = sx; /* 53191 */
int x = sx; /* -12345 */
unsigned ux = usx; /* 53191 */

printf("sx = %d:\t", sx);
show_bytes((byte_pointer) &sx, sizeof(short));
printf("usx = %u:\t", usx);
show_bytes((byte_pointer) &usx, sizeof(unsigned short));
printf("x = %d:\t", x);
show_bytes((byte_pointer) &x, sizeof(int));
printf("ux  = %u:\t", ux);
show_bytes((byte_pointer) &ux, sizeof(unsigned));

//출력 결과
sx = -12345: cf c7
usx = 53191: cf c7
x = -12345: ff ff cf c7
ux = 53191: 00 00 cf c7

1. 16비트
   • 부호 있는 값 -12345와 부호 없는 값 53191은 동일한 비트 패턴 0xCFC7을 가진다.
2. 32비트 확장
   • 부호 확장 -12345 -> 0xFFFFCFC7
   • 제로 확장 53191 -> 0x0000CFC7

short sx = -12345; /* -12345 */
unsigned uy = sx; /* Mystery! */

printf("uy = %u:\t", uy);
show_bytes((byte_pointer) &uy, sizeof(unsigned));

uy = 4294954951:  ff ff cf c7

• (unsigned)sx 는 (unsigned)(int)sx와 동일하게 처리된다.

2.2.7 Truncating Numbers

비트 확장의 반대 작업으로, 숫자의 비트 크기를 줄이는 작업이다.(비트 축소(trucation)) 비트 축소는 상위 비트를 잘라내는 과정으로, 작은 데이터 타입으로 변환할 때 발생한다.

int x = 53191;
short sx = (short)x;  /* -12345 */
int y = sx;           /* -12345 */

• x를 short로 캐스팅하면 상위 16비트를 자르고, 남은 16비트는 -12345의 2의 보수 표현이 된다.
• 다시 int로 캐스팅하면 부호 확장이 발생하여 상위 16비트를 1로 채운다.
• 결과적으로 y = -12345가 유지된다.

Unsigned Number의 비트 축소

부호 없는 숫자를 축소할 때는 나머지 연산(modulus)를 사용하여 계산할 수 있다.

x’ = x mod 2^k

• x = w-비트 숫자
• x’ = k-비트 숫자(k < w)
• 잘라낸 비트는 2_i 형태의 가중치를 가지며, i>=k일 때 나머지 연산에서 무시된다.

x = 533191, k = 16, 2¹⁶ = 65536 -> x’ = 53191 mod 65536 = 53191

• x가 16비트 내에 있으므로 값이 변경되지 않는다.

Two’s-Complement Number의 비트 축소

2의 보수 숫자는 부호 비트를 포함하므로, 비트 축소 시 부호를 고려해야 한다.

x’ = U2T_k(x mod 2^k)

• x mod 2^k : 잘라낸 후의 값
• U2T_k : 상위 비트를 부호 비트로 해석하여 부호 있는 숫자로 변환

x = 53191, k = 16, 2¹⁶ = 65536 -> x mod 65536 = 53191 -> x’ = 53191 - 65536 = -12345 비트 축소는 숫자의 값에 영향을 미칠 수 있으며, 이는 오버플로우 형태로 나타날 수 있다. 부호 없는 숫자는 단순히 상위 비트를 잘라내고, 2의 보수 숫자는 부호 비트를 새로운 상위 비트로 설정한다.

2.2.8 Advice on Signed versus Unsigned

C 언어에서는 부호 있는 값(signed)과 부호 없는 값(unsigned)의 암묵적 캐스팅이 비직관적인(nonintuitive) 동작을 초래할 수 있다. 이는 코드에 명확한 표시가 없기 때문에 프로그래머가 간과하기 쉽고, 결과적으로 디버깅이 어렵고 프로그램에 버그를 유발할 가능성을 높인다.

Unsigned의 문제점으로는 암묵적 캐스팅으로 인해 예측하기 어려운 오류와 취약점이 발생할 수 있다는 점이 있다. 이러한 이유로 대부분의 다른 언어에서는 unsigned를 지원하지 않거나 필요 이상의 복잡성을 초래한다고 간주한다.

그럼에도 불구하고 unsigned는 비트 플래그 처리, 메모리 주소 표현, 모듈러 산술, 다중 정밀도 연산 등 특정 상황에서 효과적으로 사용될 수 있다. 그러나 unsigned 타입의 사용은 가능한 최소화해야 하며, 사용 시 명확한 코드 작성과 변환 규칙에 대한 이해가 반드시 필요하다.

아래 두 연습 문제는 암묵적 캐스팅과 unsigned 데이터 타입으로 인해 발생할 수 있는 미묘한 오류를 보여준다.

문제 1

/*WARNING : This is buggy code*/
float sum_elements(float a[], unsigned length){
    int i;
    float result = 0;

    for(i=0; i<=length-1; i++) 
        result += a[i];
    return result;
}

• unsigned 데이터 타입인 length가 0-1 연산으로 인해 UMax(부호 없는 최대값)로 처리되어 for문이 종료되지 않고 a의 유효하지 않은 요소에 접근을 시도하게 되어 메모리 접근 오류가 발생한다.
• 해결 방법으로는 length를 int length 선언을 하거나, for(…; i < length; …;) 으로 반복문 작성

문제 2

/*Prototype for library function strlen*/
size_t strlen(const char *s);
...

/*Determine whether string s is longer than string t*/
/*WARNING: This function is buggy*/
int strlonger(char *s, char *t){
    return strlen(s) - strlen(t) > 0;
}

• size_t의 데이터 타입은 unsigned이다. strlen의 반환값이 unsigned 데이터 타입으로 반환되므로 뺴기 연산과, 비교 연산은 부호가 없는 산술 연산을 진행하게 된다. 만약 s가 t보다 작다면 strlen(s)-strlen(t)는 음수가 되야하지만, unsigned 타입 변환이 일어나 매우 큰 unsigned 정수가 되게된다. 즉, strlonger는 0을 반환해야하지만, 1을 반환하게 된다.
• 해결 방법은 return strlen(s) > strlen(t);