[CS:APP] Chap2 A Representing and Manipulating Information(3)-Integer Aritmetic

2.3 Integer Arithmetic

많은 초보 프로그래머들은 두 개의 양수를 더했을 때 음수가 나올 수 있다는 점과, 비교식 x < y의 결과가 x - y < 0의 결과와 다를 수 있다는 점에 놀란다. 이러한 특성은 컴퓨터 연산의 유한한 본질에서 비롯된 현상이다. 컴퓨터 연산의 세부 사항을 이해하면 프로그래머가 더 신뢰할 수 있는 코드를 작성하는데 도움을 줄 수 있다.

2.3.1 Usigned Addition

1. Unsigned Addition 특성
   • w-비트로 표현된 두 수의 합은 w+1 비트가 필요할 수 있다.
   • 고정된 비트 크기에서는 최상위 비트를 잘라내어 모듈러 연산처럼 작동한다.
2. Word Size Inflation Probelm
   • 계속된 산술 연산으로 단어 크기가 무한히 증가할 수 있다.
   • 일반적으로 프로그래밍 언어는 고정 크기 산술을 사용하여 이 문제를 제한한다.
3. 모듈러 산술 적용
   • 덧셈 연산 +_uw 정의
   • x와 y가 0<=x,y<2^w일 때, x+y의 정수 합계를 w-비트로 잘라낸 뒤, 이를 부호 없는 정수로 간주한다.

   • 모듈러 산술(modular arithmetic)의 한 형태로, x+y의 비트 표현에서 2^w-1보다 큰 가중치를 가진 비트를 버리는 방식으로 구현된다.

   • 예시
     • x=9, y=12
     • 비트 표현 : x=[ 1001 ], y=[ 1100 ]
     • 합계 : x+y=21, 비트 표현 : [ 10101 ] (5비트)
     • 최상위 비트를 버리면 [ 0101 ]이 되며, 이는 10진수로 5이다.
     • 21 mod 16 = 5와 일치

Unsigned addition +_uw

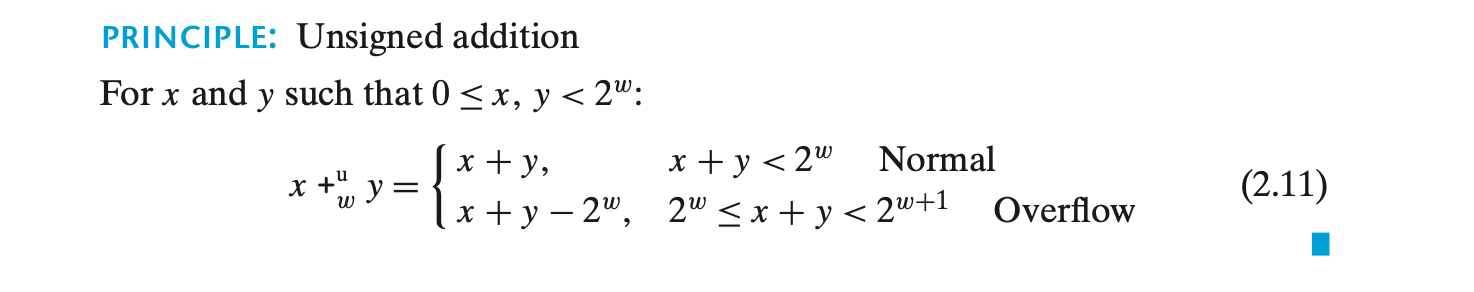
• 정상(Normal) : 덧셈 결과가 w-비트 범위 내에 있기 때문에 값을 그대로 유지한다.
• 오버플로우(Overflow) : x+y가 w-비트 범위를 초과하므로, 결과에서 2^w를 빼서 w-비트 값으로 변환한다.

Overflow

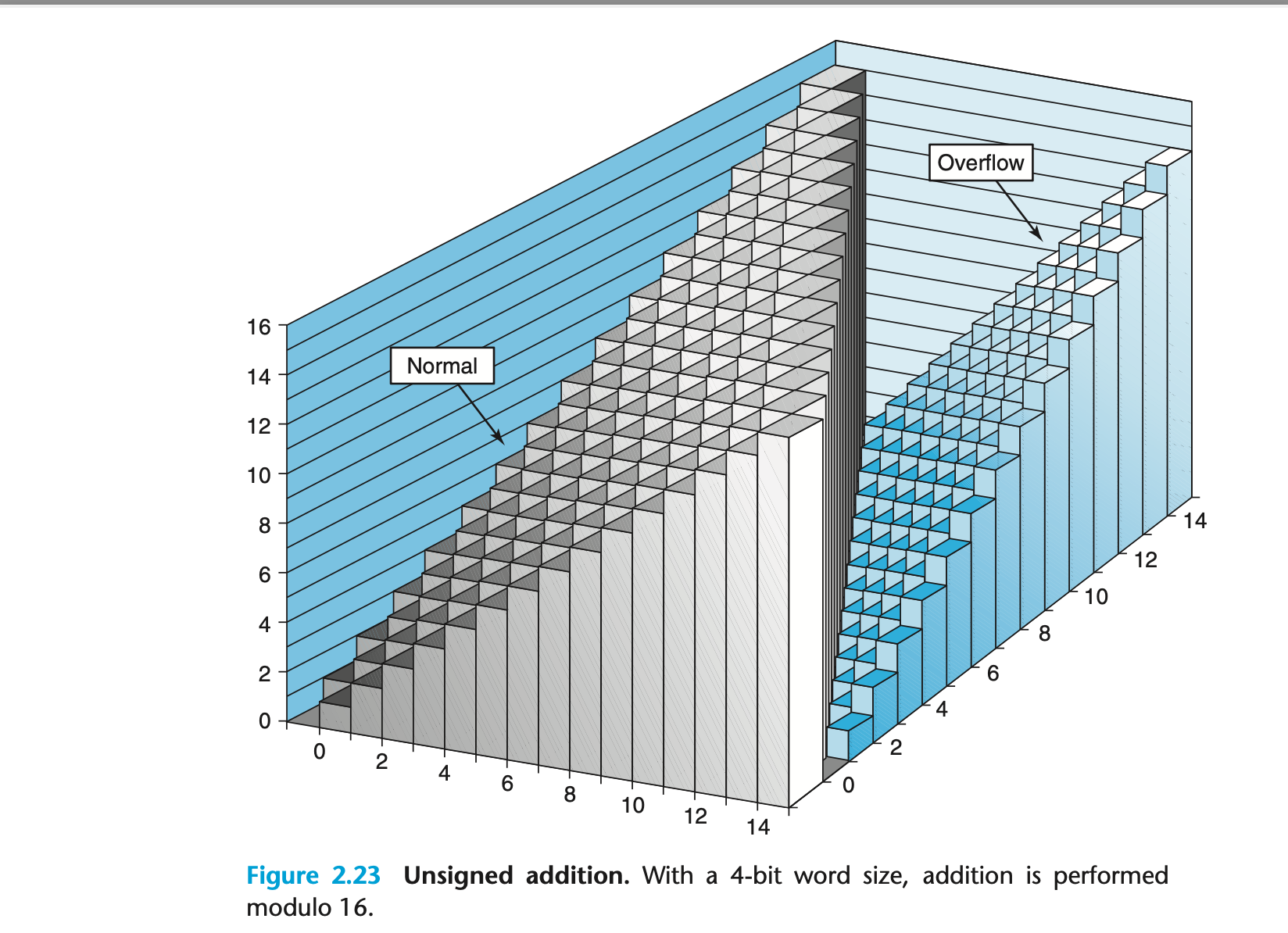
• 산술 연산(Arithmetic Operation)에서 오버플로우(Overflow)란, 연산 결과가 데이터 타입의 단어 크기(word size) 범위를 초과하여 표현할 수 없는 경우를 말한다.
• 위에 식에 따르면 오버플로우는 두 피연산자의 합이 2^w 이상일 때 발생한다.
• 위에 그림은 단어 크기 w=4인 경우의 부호 없는 덧셈 함수(Usigned Addition Function)을 보여준다.
  • x + y < 16인 경우 Normal, 덧셈 결과는 x+y와 동일
  • x + y >=16인 경우 Overflow, 결과는 x+y-16
• C 언어에서는 오버플로우가 오류로 표시되지 않는다.
• 프로그래머는 오버플로우 발생 여부를 확인해야 할 때가 있다.

오버플로우 감지

• 부호 없는 덧셈의 오버플로우 감지
  • x와 y가 0<=x,y<= UMax_w인 범위에서 s = x+_uw y라고 합을 계산한다고 가정한다.

  • s가 오버플로우했는지 확인하는 방법은, s < x, s < y인 경우 오버플로우가 발생했다고 판단

  • 예제 : 9 +_u4 12 = 5
  • 5 < 9 이므로 오버플로우 발생

Unsigned Negation

• 부호 없는 부정(Unsigned Negation)
  • 0 <= x < 2^w인 모든 x에 대해, w-비트에서의 부정은 다음과 같이 정의된다.

  

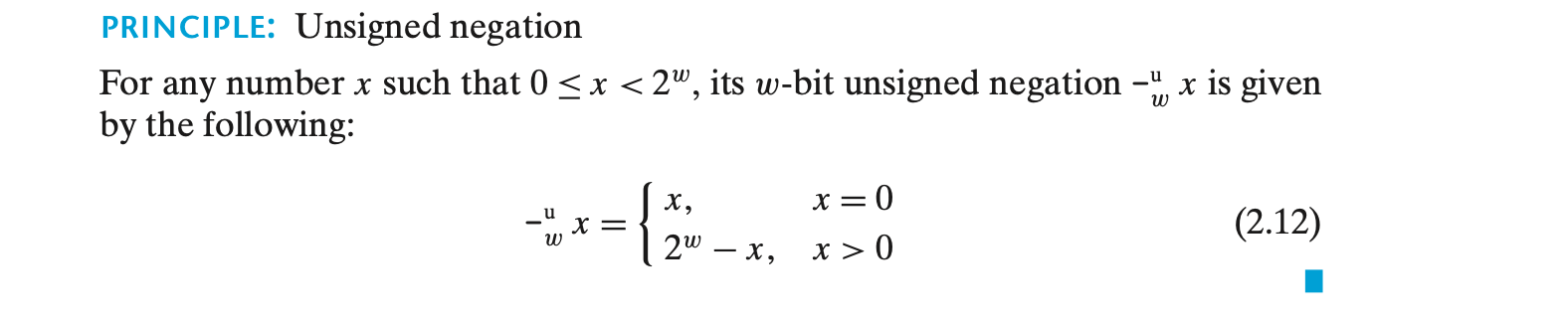
2.3.2 Two’s-Complement Addition

2의 보수 덧셈에서 결과가 표현 가능한 범위(word size w)를 벗어나면 오버플로우(overflow)가 발생한다.

정수 x와 y가 -2^w-1 <= x,y < 2^w-1 - 1의 범위에 있을 때, 합계는 -2^w <= x+y < 2^w - 2의 범위를 가질 수 있으며, 정확히 표현하려면 w+1 비트가 필요하다.

데이터를 w-비트로 유지하기 위해 오버플로우를 감지하고 결과를 조정해야 한다.

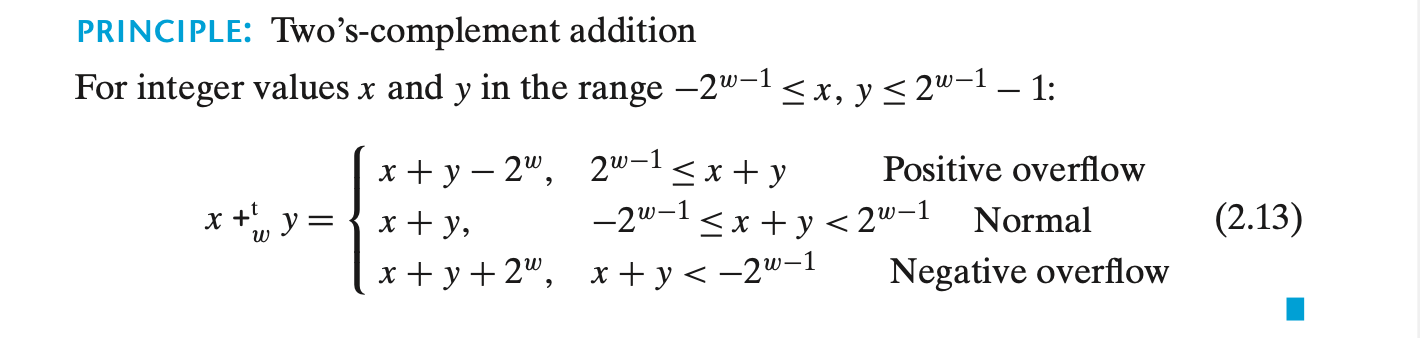
• 연산 x +_tw y는 x+y의 결과를 w-비트로 잘라낸 뒤 2의 보수 값으로 해석한 결과이다.

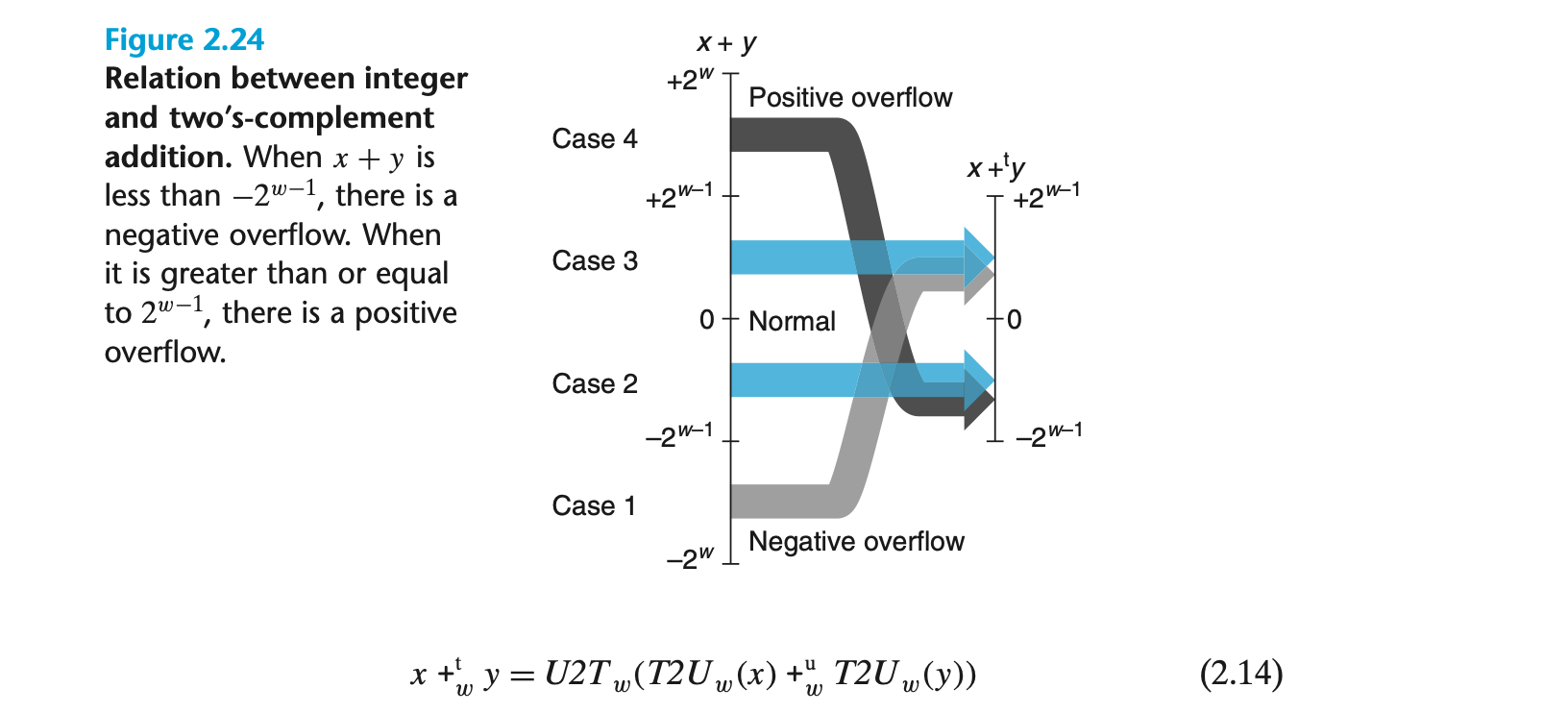
1. Case 1 : Negative Overflow
   • x + y < -2^w-1
   • 결과 : x + y + 2^w
   • 두 음수를 더한 결과가 양수가 되는 경우
2. Case 2 : Normal(Negative Sum)
   • -2^w-1 <= x + y < 0
   • 결과 : x + y 그대로 유지
3. Case 3 : Normal(Positive Sum)
   • 0 <= x + y < 2^w-1
   • 결과 : x + y 그대로 유지
4. Case 4 : Positive Overflow
   • x + y > 2^w-1
   • 결과 : x + y - 2^w
   • 두 양수를 더한 결과가 음수가 되는 경우

Overflow

오버플로우 결과 및 시각화

• 양의 오버플로우 : 결과 값에서 2^w를 뺌.
• 음의 오버플로우 : 결과 값에서 2^w를 더함.

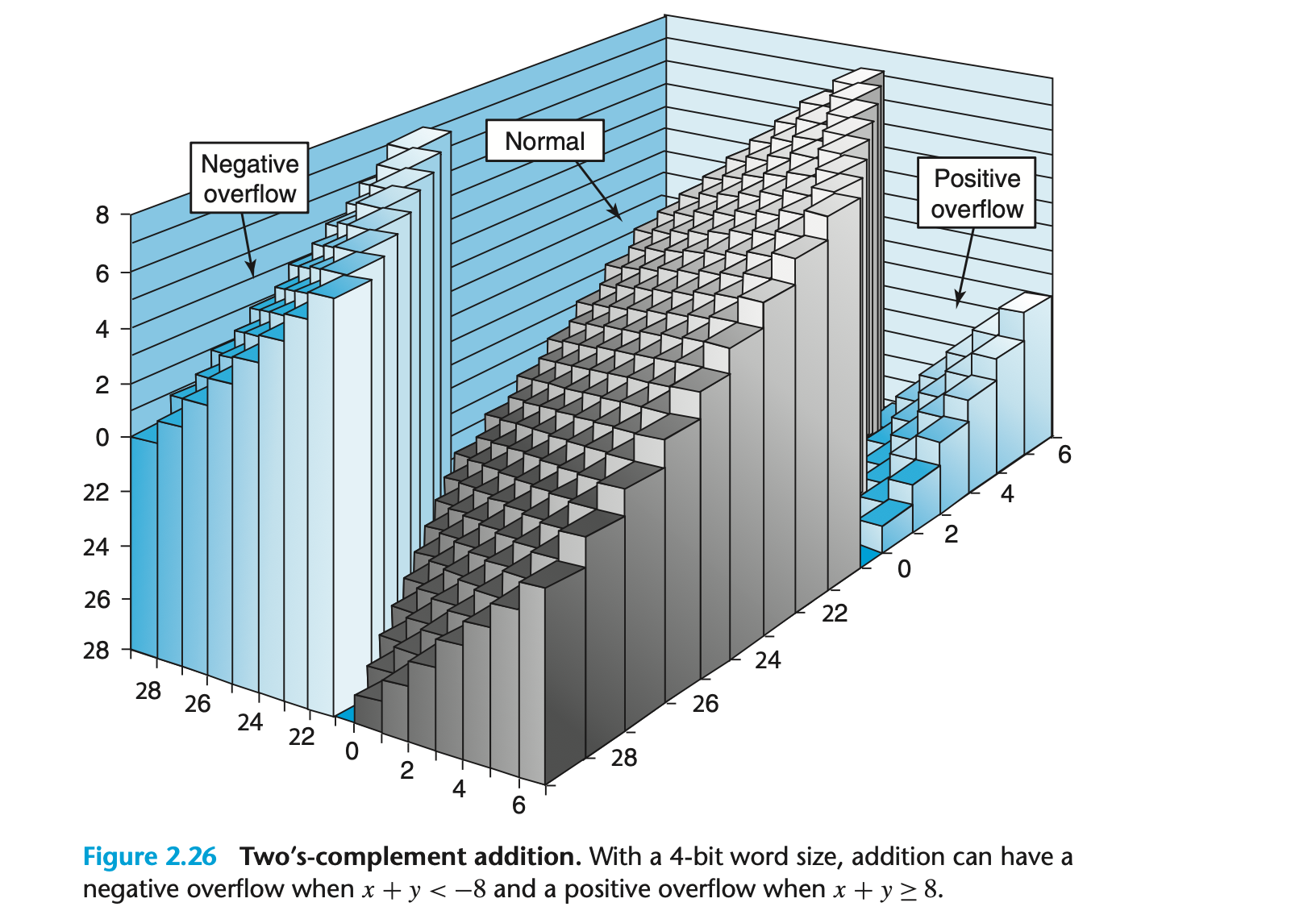
• 단어 크기 w = 4 (범위 : -8 ~ 7)
• 결과의 오버플로우:
  • x + y >= 8 : Positive Overflow(결과를 16감소)
  • x + y < -8 : Negative Overflow(결과에 16증가)
• 정상 범위 :
  • -8 <= x + y < 8 : 값 그대로 유지

오버플로우 감지 원리

• Positive Overflow(양의 오버플로우)
  • 조건 : x >= 0,y >= 0, s < 0
  • 두 양수를 더했는데 음수가 결과로 나온 경우
• Negative Overflow(음의 오버플로우)
  • 조건 : x < 0, y < 0, s >= 0
  • 두 음수를 더했는데 양수가 결과로 나온 경우

2.3.3 Two’s-Complement Negation

2의 보수에서, 범위 TMin_w <= x <= TMax_w에 있는 모든 숫자 x는 +_tw 연산에서 덧셈의 역원을 가지며, 이를 -_tw로 나타낸다.

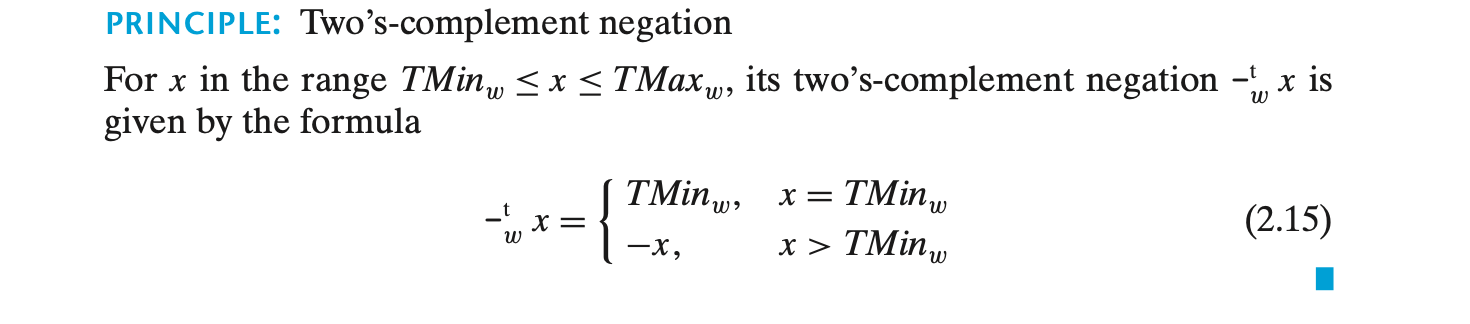
즉, w-비트 2의 보수 덧셈에서 TMin_w는 자기 자신이 덧셈의 역원이며, 나머지 모든 값 x는 -x를 덧셈의 역원으로 가진다.

2.3.4 Unsigned Multiplication

정수 x와 y가 0 <= x,y <= 2^w - 1 범위에 있다면, 이들은 w-비트, 부호 없는 숫자로 표현될 수 있다. 그러나 이들의 곱 x*y에서 (2^w - 1)² 범위까지 확장될 수 있으며, 이를 정확히 표현하려면 2w-비트가 필요하다.

C 언어에서는 부호 없는 곱셈이 2w-비트 정수 곱의 하위 w-비트 값을 결과로 반환하도록 정의된다. x *_uw y로 나타낸다.

부호 없는 숫자를 w-비트로 잘라내는 것은 2^w로 모듈러 연산을 수행하는 것과 동일하다.

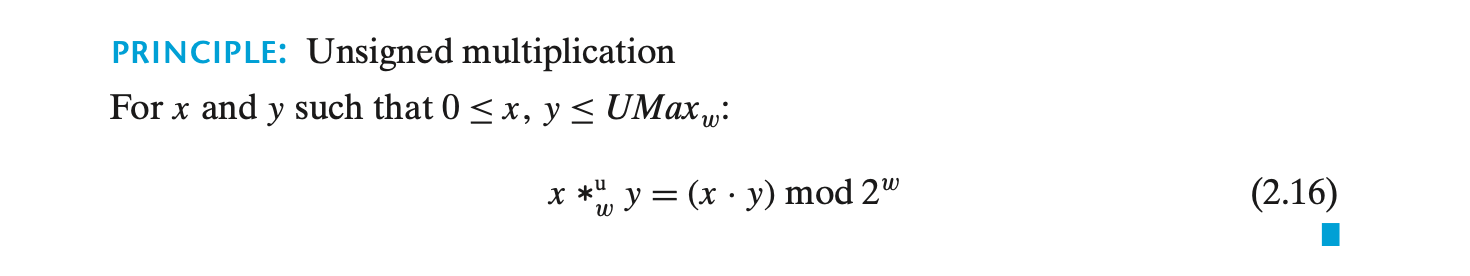
2.3.5 Two’s-Complement Multiplication

정수 x와 y가 -2^w-1 <= x, y <= 2^w-1 - 1 범위에 있다면, 이들은 w-비트 2의 보수 숫자로 표현될 수 있다. 하지만 이들의 곱도 마찬가지로 정확히 표현하려면 2w-비트가 필요하다.

C언어에서는 부호 있는 곱셈은 일반적으로 2w-비트 곱의 결과를 w-비트로 잘라내는(Truncating) 방식으로 수행된다. 이 값을 x *_tw y로 나타낸다.

2의 보수 숫자를 w-비트로 잘라내는 것은 먼저 2^w로 모듈러 연산을 수행한 후, 부호 없는 값을 2의 보수 형태로 변환하는 것이다.

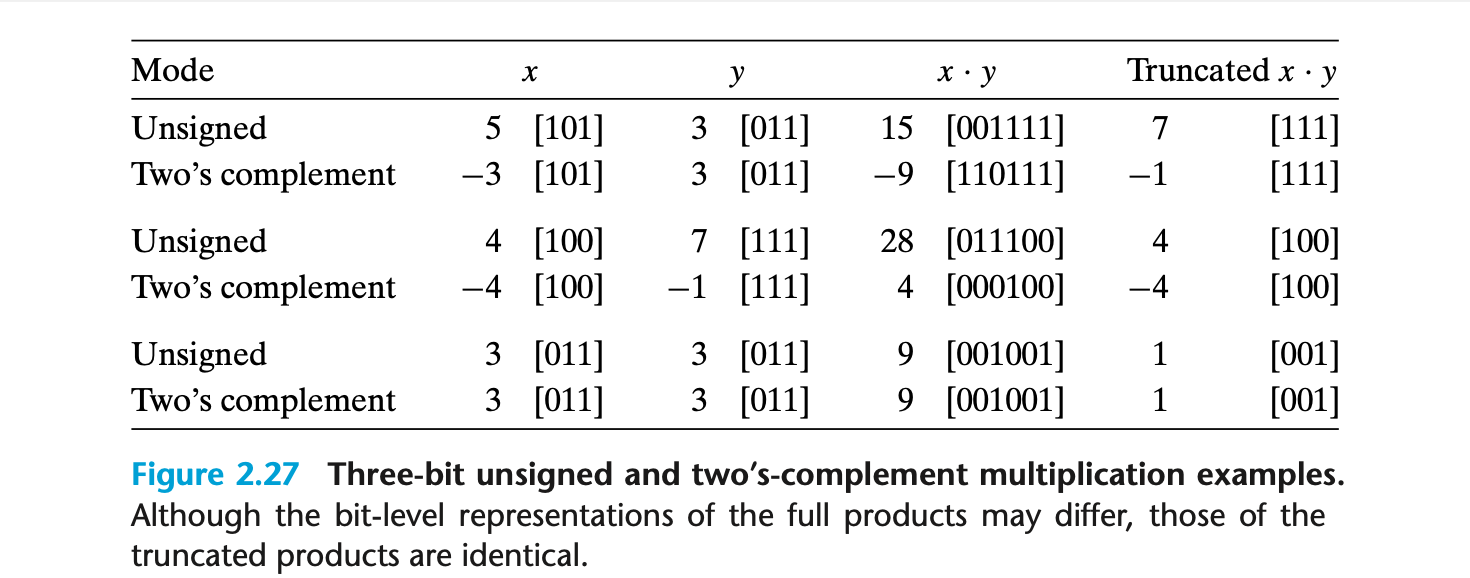
곱셈 연산의 비트 단위 표현이 Unsigned 와 Two’s-complement 모두에서 동일함은 아래에서 설명이 된다.

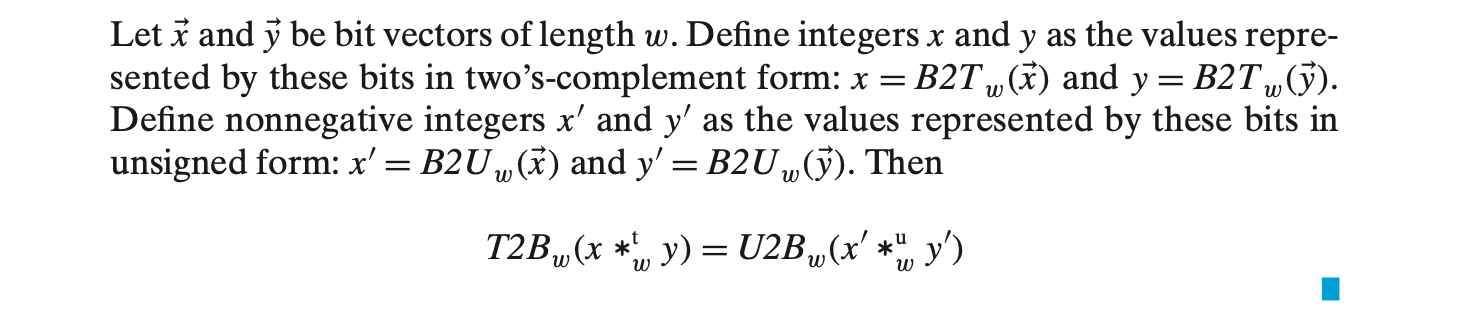
2.3.6 Multiplying by Constants

과거에는 정수 곱셈(integer multiply) 연산이 느렸으며, 10개 이상의 클록 사이클이 필요했지만, 덧셈, 뺄셈, 비트 연산, 시프트 연산 등은 1개의 클록 사이클로 처리되었다.

현재의 Intel Core i7 Haswell에서도 정수 곱셈은 여전히 3개의 클록 사이클이 필요하다.

이러한 이유로 컴파일러는 곱셈을 시프트(shift)와 덧셈(addition) 조합으로 대체하여 성능을 최적화하려고 시도한다.

2의 거듭제곱으로 곱하기

2의 거듭제곱으로 곱하기

• x가 부호 없는 정수라고 할 때, x2^k는 x의 비트 패턴 오른쪽에 k개의 0을 추가한 것과 동일하다.

• ex. x = 11(w=4일 때 비트 패턴 : [1011])
  • k=2만큼 왼쪽으로 시프트하면 6비트 벡터 [101100]이 되고, 이는 11*4=44를 나타낸다.

• 고정 크기에서의 시프트 : 고정된 단어 크기에서 k만큼 왼쪽 시프트하면 상위 k비트가 버려진다. 결과는 w-비트 내에서의 2의 거듭제곱 곱셈과 동일하다.

• 부호 없는 값 x와 k에 대해 x « k는 x *_uw 2^k를 나타낸다.
• 2의 보수 값에서도 동일하게 적용된다. x *_tw 2^k

곱셈과 시프트의 오버플로우

• 2의 거듭제곱 곱셈은 부호 없는 산술이나 2의 보수 산술 모두에서 오버플로우를 일으킬 수 있다.
• [1011] (x=11)을 k=2만큼 시프트 -> [101100] (x=44)
• 결과를 w=4 비트로 자르면 [1100] (x=12), 44 mod 16 = 12와 동일

곱셈을 시프트와 덧셈으로 대체

• 곱셈 최적화
• ex. x * 14
  • 14 = 2³ + 2² + 2¹
  • 컴파일러는 x*14를 (x«3) + (x«2) + (x«1)로 변환
  • 곱셈 1번 -> 시프트 3번, 덧셈 2번으로 대체
• 최적화 ex. x * 14
  • 14 = 2⁴ - 2¹
  • x*14 = (x«4) - (x«1)
  • 곱셈 1번 -> 시프트 2번, 뺄셈 1번으로 최적화

특정 곱셈 패턴과 LEA 명령어

• LEA 명령어는 특정 곱셈을 (a « k) + b 형태로 최적화 가능
  • k = 0,1,2,3,b는 0이거나 특정 값일 수 있음.
  • ex. 3*a = (a « 1) + a
• k와 b 조합을 사용해 특정 정수 곱셈을 시프트와 덧셈으로 대체 가능

임의 상수 곱셈 최적화

• 상수 K를 이진 표현으로 나타내면, K는 0과 1의 교대 시퀀스로 표현 가능

• ex. K = 14 = [ 0…0 ][ 111 ][0] (n=3, m=1)

• 최적화 형태
  • Form A : (x « n) + (x « (n-1)) + … + (x « m)
  • Form B : (x « (n+1)) - (x « m)
• 상수 K의 모든 비트 시퀀스를 위 두 형태로 변환하여 곱셈 없이 계산
• 단, 실제 최적화 여부는 명령어 간 속도 차이에 따라 결정
  • ex. x*K에서 시프트, 덧셈, 뺄셈 조합이 적은 경우에만 최적화 수행

2.3.7 Dividing by Powers of 2

정수 나눗셈은 정수 곱셈보다 느리며, 대부분의 머신에서 30개 이상의 클록 사이클이 소요된다.

2의 거듭제곱으로 나누기는 왼쪽 시프트 대신 오른쪽 시프트(right shift)를 사용하여 구현 가능하다.

• 부호 없는 숫자는 논리적 시프트(logical shift)
• 2의 보수 숫자는 산술적 시프트(arithmetic shift)

정수 나눗셈의 기본 원칙

부호 없는 나눗셈

2.3.8 Final Thoughts on Integer Arithmetic

컴퓨터가 수행하는 “정수” 산술은 실제로는 모듈러 산술의 한 형태이다. 숫자를 표현하는 데 사용되는 유한한 워드 크기는 가능한 값의 범위를 제한하며, 이로 인해 연산 중에 오버플로우(overflow)가 발생할 수 있다. 또한 2의 보수 표현(Two’s-Complement representation)은 동일한 비트 수준 구현을 사용하면서 양수와 음수를 모두 표현할 수 있는 방법을 제공한다. 덧셈, 뺄셈, 곱셈, 나눗셈과 같은 연산은 피연산자가 부호 없는(Unsigned) 형태인지 2의 보수 형태인지에 관계없이 동일하거나 매우 유사한 비트 수준 동작을 가진다.

C언어에서 일부 예상치 못한 결과를 초래함을 확인했다. 이는 인식하기 어려운 버그의 원인이 될 수 있다. 특히 Unsigned data type이 개념적으로는 단순해 보이지만, 숙련된 프로그래머조차 예상하지 못한 동작을 초래할 수 있음을 확인했다. 또한 이 데이터 타입은 예기치 않은 방식으로 나타날 수 있음을 확인했다. 예를 들어, 정수 상수를 작성할 때나 라이브러리 루틴을 호출할 때 이러한 경우가 발생할 수 있다.