[CS:APP] Chap2 A Representing and Manipulating Information(4)-Floating Point

2.4 Floagting Point

2.4.1 Fractional Binary Numbers

1. 이진 소수 표현

• 소수점 왼쪽의 비트는 2ⁱ의 가중치를 가지며, 오른쪽 비트는 2^-i의 가중치를 가진다.

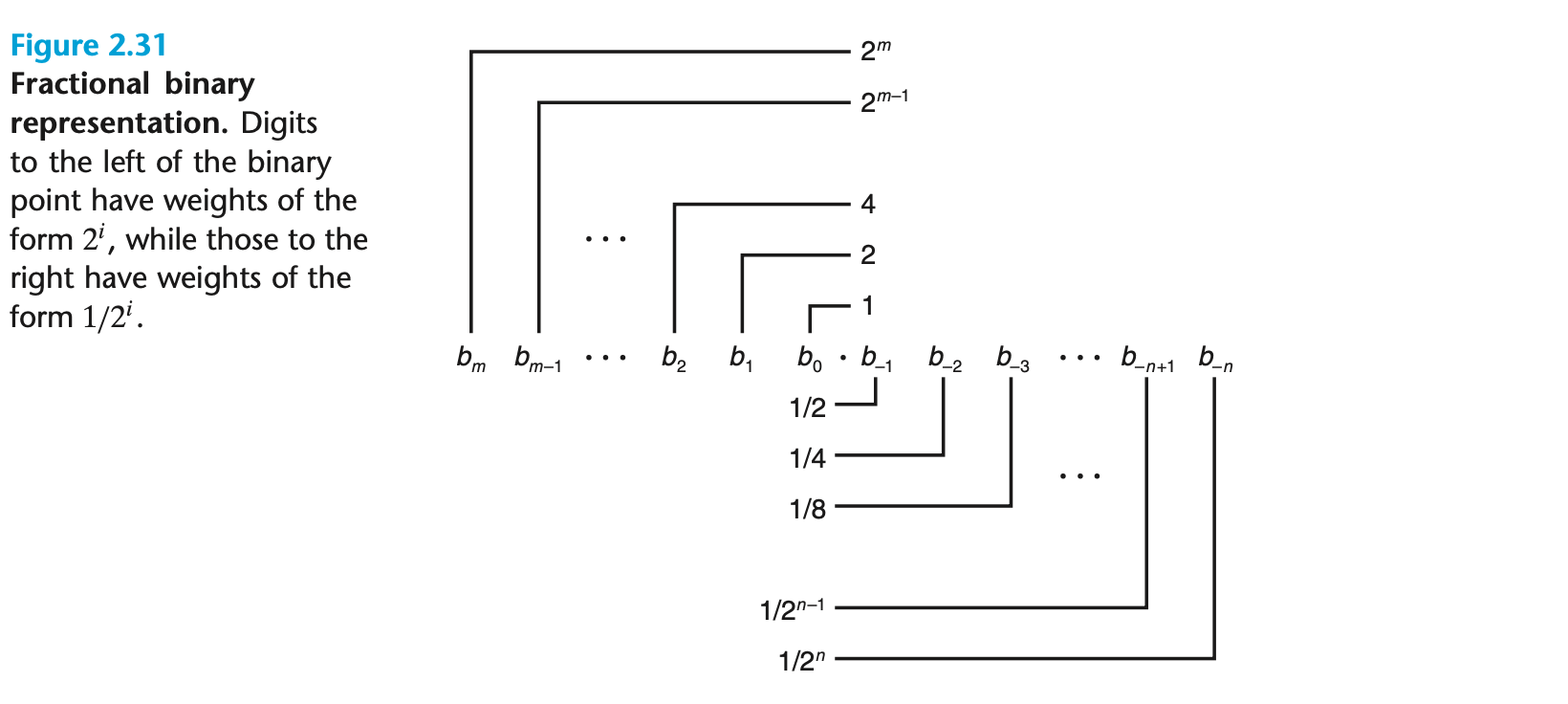
• 101.11₂ 표현
  • 1 x 2² + 0 x 2¹ + 1 x 2⁰ + 1 x 2^-1 + 1 x 2^-2 = 4 + 0 + 1 + 1/2 + 1/4 = 23/4

2. 소수점 이동

• 이진수에서 소수점을 왼쪽으로 한 칸 이동하면 숫자는 /2, 오른쪽으로 이동하면 X2
• 101.11₂ -> 10.111₂ : 5.75

3. 근사치와 제한

• 이진 소수는 X x 2^y 형태로 표현할 수 있는 숫자만 정확히 나타낼 수 있다.
• 위 형태로 정확히 표현할 수 없으면, 근사치로 나타낸다.

2.4.2 IEEE Floating-Point Representation

1. 표현 방식

• IEEE 부동소수점 표현 : V = (-1)^s x M x 2^E
  • s : 부호 비트(양수: s=0, 음수: s=1)
  • M : 유효 숫자(significand), 정규화된 경우 1<= M < 2
  • E : 지수(Bias 사용)

단정밀도(32비트)

• 1비트 s, 8비트 지수 exp, 23비트 유효숫자 frac
• bias값: 127

배정밀도(64비트)

• 1비트 s, 11비트 지수 exp, 52비트 유효숫자 frac
• bias 값 : 1023

값의 분류

1. 정규화 값(Nomalized Values)
   • exp != 0, exp != 255
   • E = e - bias
   • M = 1 + f (1<= M < 2) (추가 비트 정밀도 확보)
2. 비정규화 값(Denomalized Values)
   • 0.0에 매우 가까운 숫자 표현(gradual Underflow)
   • exp field 모두 0
   • E = 1 - bias
   • M = f(implied leading 제외된 값)
   • 부호 비트가 0과 1일로 +0.0 , -0.0 두가지의 0값 존재 : 해당 값은 같은 값 또는 다른 값으로 고려될 수 있음
3. 특수 값(Special Value)
   • exp field 모두 1
   • INFINITY : fraction field가 모두 0인 경우 무한대
     • 부호 비트에 따라 음의 무한대, 양의 무한대 가능
   • NaN(Not a Number) : fraction field가 0이 아닌 경우
     • 실수가 아닌 수(허수)를 표현
   • 초기화 되지 않은 데이터를 나타내기 위해 사용 가능

2.4.3 Example Numbers

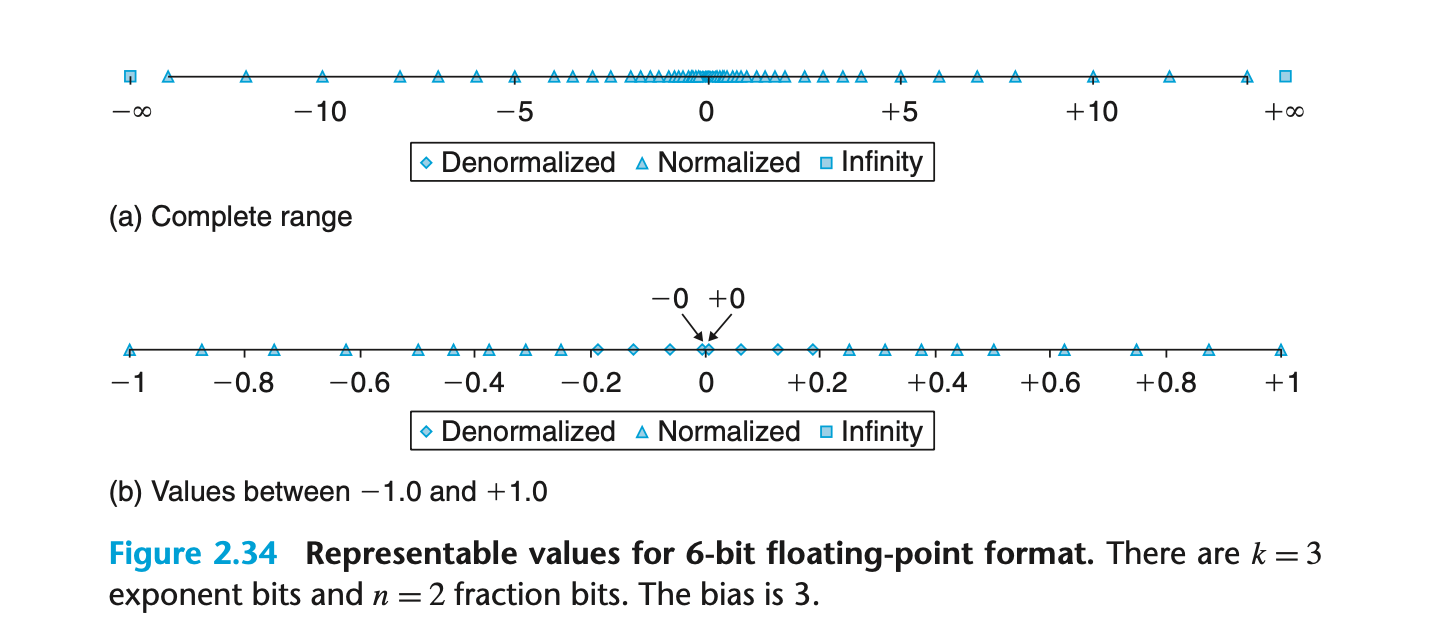
• 위 그림은 k=3 지수 비트와 n=2 유효숫자 비트를 가진 가상의 6비트 형식에서 표현할 수 있는 값들의 집합을 보여준다.
• Bias 값은 2^3-1 - 1 = 3 이다.
• (a) 부분은 NaN을 제외한 모든 표현 가능한 값을 보여준다.
• 무한대는 양쪽 끝에 위치한다.
• 최대 크기의 정규화된 숫자는 -14, +14이다.
• 비정규화된 숫자들은 0 근처에 밀집되어 있다. 이는 (b)부분에서 더 명확히 볼 수 있다.
• 표현 가능한 숫자들이 균일하게 분포되어 있지 않다는 것을 알 수 있다.
• 원점 근처에서 더 밀도가 높은 형태이다.

부동 소수점 표현의 일반적인 속성

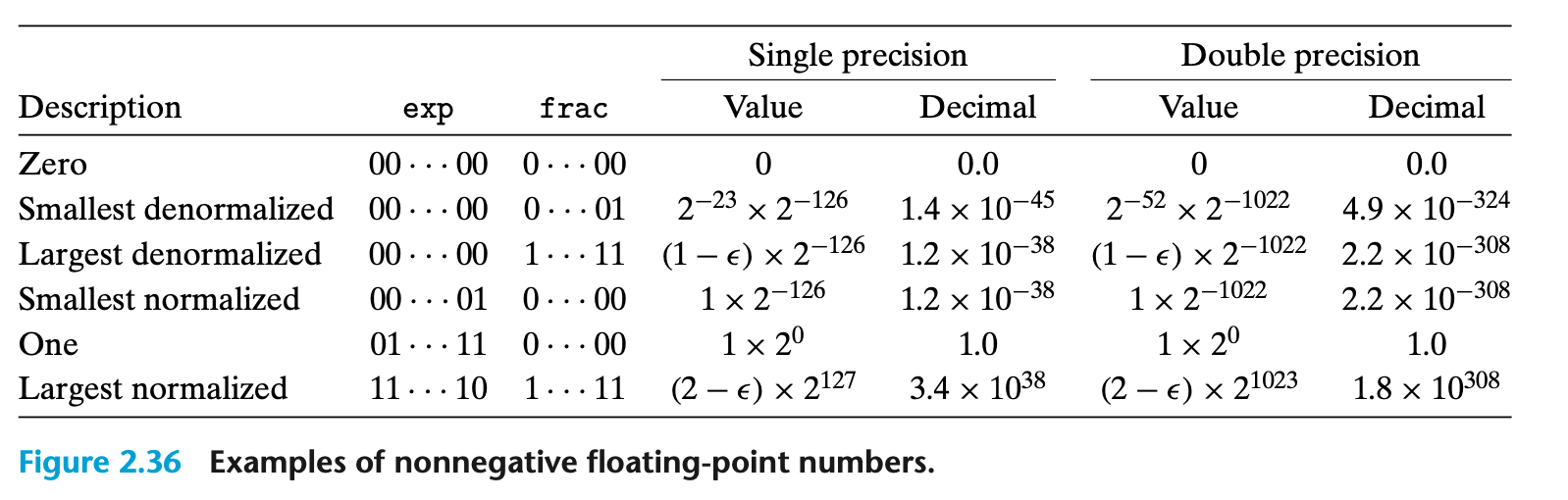
• +0.0은 모든 비트가 0이다.
• 가장 작은 Positive 비정규화 값은 LSB는 1이고 나머지는 모두 0으로 표현된다.
• 가장 큰 비정규화 값은 지수 필드는 모두 0이고 유효숫자 필드는 모두 1로 표현된다.
• 가장 작은 양의 정규화 값은 지수 필드의 최하위 비트는 1이고, 나머지는 모두 0이다.
• 값 1.0은 지수 필드는 최상위 비트를 제외하고 모두 1이고, 나머지 비트는 모두 0이다.
• 가장 큰 정규화 값은 부호 비트는 0, 지수 필드의 최하위 비트는 0, 나머지는 모두 1이다.

2.4.4 Rounding

부동 소수점 연산은 유한한 표현으로 인해 실수 연산의 근사치를 구한다.

반올림 4가지 방식

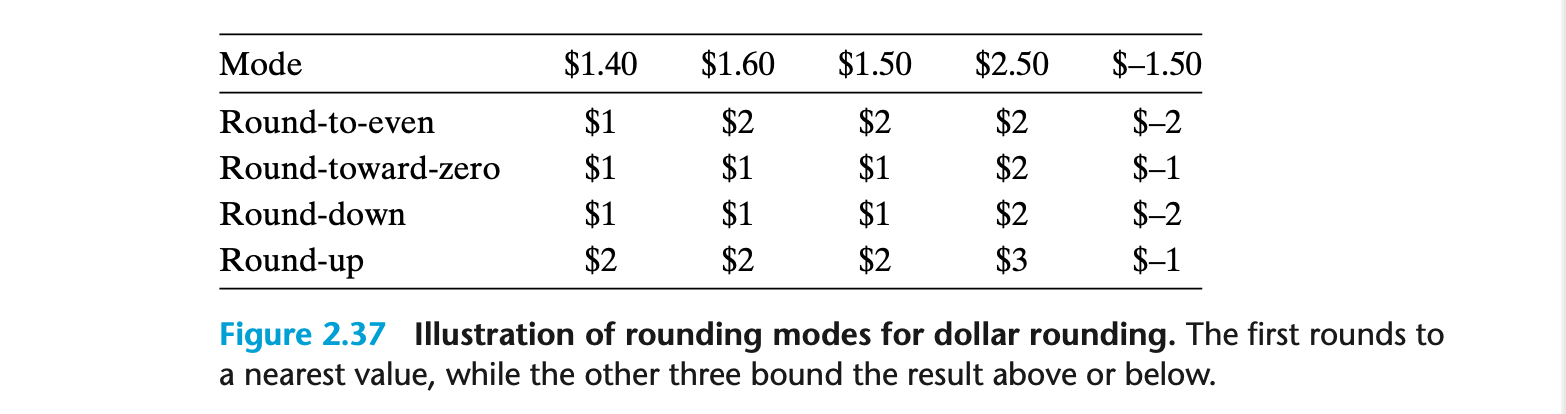
• Round-toward-zero mode : 양수는 내림, 음수는 올림
• Round-down mode : 양수 음수 모두 내림(현재 값보다 항상 작음)
• Round-up mode : 양수 음수 모두 올림(현재 값보다 항상 증가)

• Round-to-even : 가장 가까운 값으로 반올림하며, 중간값(절반)인 경우 짝수로 반올림(마지막 자리수만 홀수인지 짝수인지만 확인하면됨)

• 통계적 편향을 줄이기 위해 Round-to-even방식이 사용됨

2.4.5 Floating-Point Operations

1. 덧셈과 곱셈의 특성
   • 덧셈
   • 교환 법칙(Commutativity)을 만족하지만, 결합법칙(Associativity)은 만족하지 않음
   • (3.14+1e10)-1e10 = 0.0
   • 3.14+(1e10- 1e10) = 3.14

• 곱셈
  • 교환법칙을 만족하지만, 결합법칙과 분배법칙은 만족하지 않음
  • (1e201e20)1e-20 = +∞
  • 1e20(1e201e-20) = 1e20

결합법칙과 분배법칙의 부재는 계산 정확도와 효율성에 영향을 미친다. 예를 들어 3차원 공간에서 두 선이 교차하는지 확인하는 코드는 단순해 보이지만 복잡한 문제가 될 수 있다.

2.4.6 Floating-Point in C

1. C언어의 부동소수점 데이터 타입
   • float (단정밀도)
   • double (배정밀도)
   • IEEE 부동 소수점을 사용하는 머신에서 기본 round-to-even 반올림 모드 사용
2. 특수 값 처리
   • +∞,−∞,NaN 등의 특수 값은 시스템마다 구현 방식이 다름.
3. 형 변환
   • int -> float : 반올림 가능, 오버플로우 없음
   • int/float -> double : 정확히 변환 가능
   • double -> float : 오버플로우 가능, 반올림 발생
   • float/double -> int : Round-toward-zero, 오버플로우 가능
     • 부동소수점에서 정수로 변환 시 오버플로우가 발생하면 비정의된 결과를 생성한다.
     • ex. (int) +1e10 → -21483648