[자료구조] 재귀(Recursion)

재귀 함수는 “자기 자신을 호출하는 함수”를 의미한다. 간결하고 효율적인 코드를 작성하는 데 유용하다. 특히 트리나 그래프와 같은 계층적 구조의 탐색, 분할 정복 알고리즘, 그리고 복잡한 수학적 계산에서 자주 사용된다.

재귀를 제대로 이해하기 위해서는 단순히 “함수가 자기 자신을 호출한다”는 개념을 넘어, 메모리에서 스택(Stack)이 재귀함수와 어떻게 작동하는지 알아야 한다. 재귀 함수는 호출될 때마다 메모리의 스택 영역을 사용하여 현재 함수 호출 상태를 저장하며, 이는 재귀 함수가 중단된 시점에서 다시 실행을 이어갈 수 있는 원동력이 된다.

이 글에서는 먼저 스택 메모리와 재귀 함수의 관계를 살펴보고, 이를 바탕으로 재귀 함수의 기본적인 구조와 동작 원리를 이해할 예정이다. 이후에는 간단한 예제와 함께, 재귀가 실질적으로 코드에서 어떻게 활용되는지를 다뤄볼 것이다.

스택(Stack)

스택 메모리는 가상 메모리(Virtual Memory)의 일부이다. 스택 메모리는 프로그램 실행 중 함수 호출과 관련된 데이터를 저장하는 메모리 공간이다. 스택 메모리는 LIFO(후입선출) 구조를 따른다. 메모리 구조상 위에서 아래로 공간을 차지하고 있다.

아래 그림은 함수가 호출될 때 스택 메모리에서 일어나고 있는 상황을 표현한 것이다. 스택 메모리에서는 함수가 호출될 때마다 각 함수의 실행 정보(스택 프레임)가 생성(push)되며, 일반적으로 위에서 아래로(높은 메모리 주소에서 낮은 메모리 주소로) 쌓여 내려가는 방식으로 스택 프레임이 추가된다.

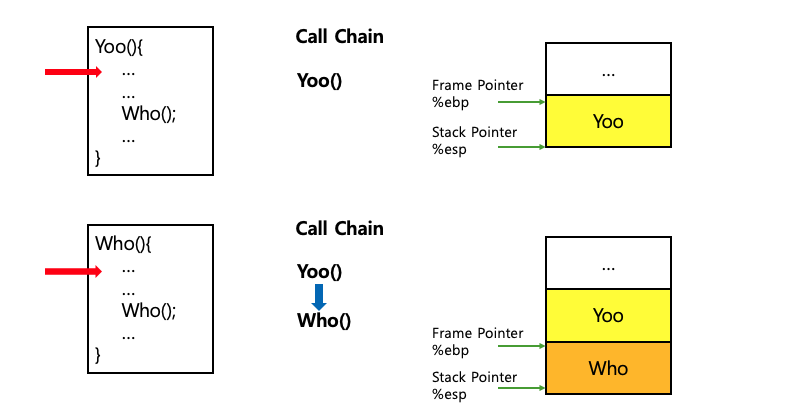
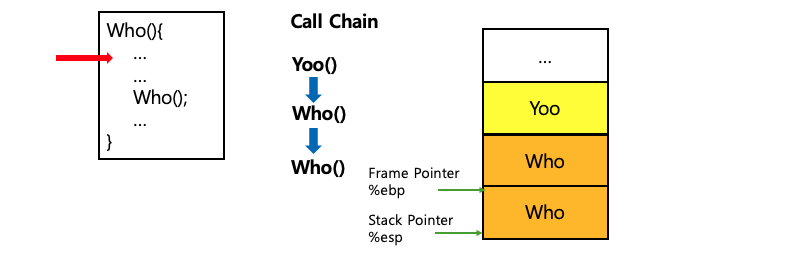
함수가 종료되면 해당 함수에 대한 스택 프레임이 스택에서 제거(pop)되어 메모리 공간이 해제된다. 이는 스택의 LIFO 구조에 따라 가장 최근에 호출된 함수의 스택 프레임부터 제거되는 방식이다.

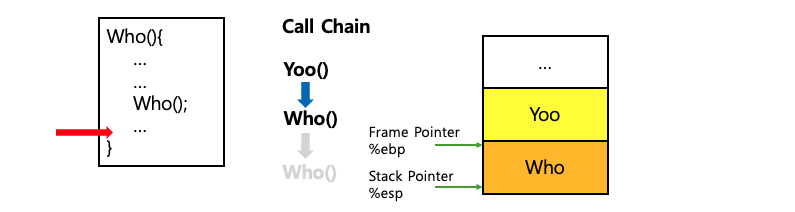
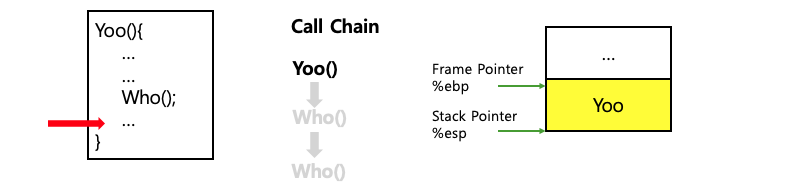
위 그림에서 알 수 있듯이 함수들은 호출될 때 새로운 스택 프레임을 생성하여 독립적으로 실행된다. 함수가 반환될 때, 코드의 위치와 스택 프레임의 상태를 이해하면 재귀 함수의 작동 원리를 훨씬 쉽게 파악할 수 있다. (스택 메모리, 가상 메모리 등에 관련한 자세한 내용은 아래 링크 참고)

재귀(Recursion)에 대한 기본적인 이해

다시 한번 말하지만, 재귀는 자기 자신을 호출하는 함수이다. 재귀 함수는 복잡한 문제를 더 작은 부분 문제로 나누어 해결하는 분할 정복(Divide and Conquer) 방식에 적합하며, 프로그래밍에서 반복적인 작업을 처리하거나, 계층적 구조를 탐색할 때 자주 사용된다.

재귀 함수의 기본 구조

• 기저 조건(Base Case) : 재귀 호출을 멈추는 조건(탈출 조건)이다. 이 조건을 충족하면 함수가 더 이상 자기 자신을 호출하지 않고 반환한다. 기저 조건이 없으면 무한 루프가 발생하고, 결국 스택 오버플로(Stack Overflow)가 발생한다.

• 재귀 호출(Recursive Call) : 함수가 자기 자신을 호출한다. 각 호출은 새로운 스택 프레임을 생성하여 독립적으로 실행된다.

예제: 팩토리얼 계산

 #include <stdio.h>

 int Factorial(int n){
    if(n==0) return 1;//기저 조건
    else return n * Factorial(n-1);//재귀 호출
 }

 int main(void){
    printf("5! = %d \n", Factorial(5));//출력 120
    return 0;
 }

재귀 함수의 동작 방식

• 스택 메모리에서의 동작
  1. 함수가 호출될 때마다 새로운 스택 프레임(Stack Frame)이 생성되어 함수의 매개변수, 지역 변수, 복귀 주소 등을 저장한다.
  2. 재귀 호출은 각 호출의 상태를 스택에 저장하면서 진행된다.
  3. 기저 조건을 만족하면 반환이 시작되고, 스택에 저장된 각 호출 상태(스택 프레임)가 제거되면서 계산이 완료된다.
• 팩토리얼 예제의 동작 과정
  1. Factorial(3) 호출 -> 스택에 저장 : n=3
  2. Factorial(2) 호출 -> 스택에 저장 : n=2
  3. Factorial(1) 호출 -> 스택에 저장 : n=1
  4. Factorial(0) 호출 -> 반환: 1 -> 계산 시작
  5. Factorial(1) 반환 -> 반환: 1(1x1)
  6. Factorial(2) 반환 -> 반환: 2(2x1)
  7. Factorial(3) 반환 -> 반환: 6(3x2)
• 재귀 함수의 장단점
  • 장점
    • 코드가 직관적이고 간결해진다.
    • 트리, 그래프 등 계층적 구조를 탐색하거나 분할 정복 알고리즘에 적합하다.
    • 문제를 작은 단위로 나누는 데 용이하다.
  • 단점
    • 스택 오버플로 위험 : 재귀 깊이가 너무 깊어지면 스택 메모리를 초과하여 프로그램이 비정상 종료될 수 있다.
    • 비용 문제 : 재귀 호출은 반복문에 비해 오버헤드가 크다(스택 프레임 생성 및 제거 비용)

재귀의 활용

피보나치 수열 : Fibonacci Sequence

피보나치 수열은 재귀적인 형태를 띠는 대표적인 수열로서 다음과 같이 전개 된다.

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 ...

쉽게 말해 ‘앞에 두 개 더해서 현재의 수를 만들어가는 수열’이다. 때문에 처음 두 개의 수 0과 1이 주어진 상태에서 수를 만들어 가게 된다. 즉, 수열의 “n번째 값 = 수열의 n-1번째 값 + 수열의 n-2번째 값”이 된다. 아래는 피보나치 수열 코드이다.

#include <stdio.h>

int Fibo(int n){
    if(n==1) return 0;
    else if(n==2) return 1;
    else return Fibo(n-1) + Fibo(n-2); //재귀 호출
}

int main(void){
    int i;
    for(i=1; i<15; i++)
        printf("%d", Fibo(i));

    return 0;
}

그렇다면 코드의 실행 흐름은 어떤지 살펴보자. 아래는 Fibo 함수의 호출 순서를 정리하기 위한 코드이다.

 #include <stdio.h>
 
 int Fibo(int n){
    printf("func call param %d \n", n);

    if(n==1) return 0;
    else if(n==2) return 1;
    else return Fibo(n-1) + Fibo(n-2); //재귀 호출
 }

 int main(void){
    Fibo(7);
    return 0;
 }

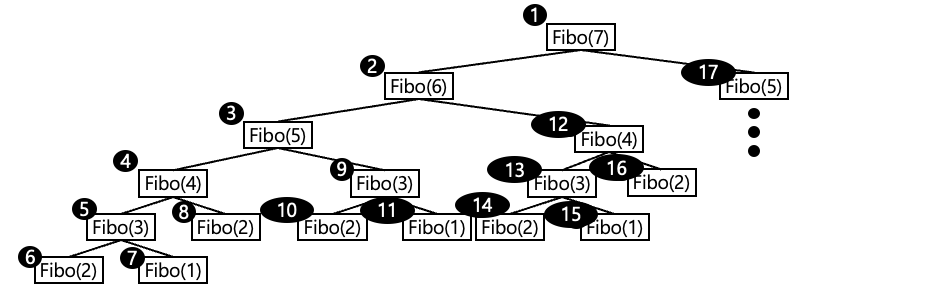
위 예제에서 보이듯이 재귀함수는 매우 많은 수의 함수 호출을 동반한다. 피보나치 수열의 7번째 값의 출력을 위해서도 25회의 함수 호출이 동반되었다. 때문에 성능상의 불리함은 분명 존재한다. 그럼 어떠한 순서대로 함수의 호출이 진행이 되는지 정리해보자.

main 함수가 호출되면 Fibo 함수가 호출되면서 인자로 7이 전달되고, 이어서 Fibo 함수 내에 존재하는 다음 문장이 실행된다.

 return Fibo(n-1) + Fibo(n-2); //Fibo(6) + Fibo(5)

즉, 두 개의 Fibo 함수가 다시 호출되는데, + 연산자의 왼편에 있는 Fibo 함수 호출이 완료되어야 비로소 + 연산자의 오른편에 있는 Fibo 함수 호출이 진행된다. 때문에 다음의 순서대로 재귀적으로 함수의 호출이 진행된다.

이진 탐색 알고리즘의 재귀적 구현

이진 탐색 알고리즘이란?

• 이진 탐색(Binary Search)은 정렬된 배열이나 리스트에서 특정 값을 효율적으로 찾기 위해 사용되는 알고리즘이다.
• 동작 원리
  1. 중간값 선택 : 배열의 중간값을 선택한다.
  2. 비교 : 찾고자 하는 값(target)과 중간값을 비교한다.
     • target == 중간값 : 찾는 값을 발견한 경우
     • target < 중간값 : 찾는 값이 중간값보다 작으면, 중간값의 왼쪽 부분 배열에서 탐색을 계속한다.
     • target > 중간값 : 찾는 값이 중간값보다 크면, 중간값의 오른쪽 부분 배열에서 탐색을 계속한다.
  3. 반복 : 위 과정을 배열의 탐색 범위가 하나로 줄어들 때까지 반복한다.
  4. 값 없음 : 배열을 모두 탐색했음에도 값을 찾지 못한 경우, 해당 값은 배열에 없다.

이진 탐색은 데이터가 오름차순 또는 내림차순으로 정렬되어 있어야만 사용할 수 있다.

아래는 이진 탐색 알고리즘을 재귀적으로 구현한 코드이다.

#include <stdio.h>

int BSearchRecursive(int ar[], int first, int last, int target){
    int mid;
    if(first>last) return -1; //-1 반환은 탐색의 실패를 의미한다.
    mid=(first+last)/2; //탐색 대상의 중간값 찾기

    if(ar[mid] == target) return mid; //탐색된 타켓의 인덱스 값을 반환
    else if(target<ar[mid]) return BSearchRecursive(ar, first, mid-1, target); 
    //target이 중간값보다 작으면 왼쪽 부분으로 탐색 범위를 줄이고 탐색
    //왼쪽 부분으로 탐색 범위를 줄이기 위해 기존 last자리를 mid-1 로 대체
    else return BSearchRecursive(ar, mid+1, last, target);
    //target이 중간값보다 크면 오른쪽 부분으로 탐색 범위를 줄이고 탐색
    //오른쪽 부분으로 탐색 범위를 줄이기 위해 기존 start자리를 mid+1로 대체
}

int main(void){
    int arr[]={1,3,5,7,9};
    int idx;

    idx=BSearchRecursive(arr, 0, sizeof(arr)/sizeof(int)-1, 7);
    if(idx == -1) printf("탐색 실패\n");
    else printf("타켓 저장 인덱스 : %d \n", idx);

    idx=BSearchRecursive(arr, 0, sizeof(arr)/sizeof(int)-1, 4);
    if(idx == -1) printf("탐색 실패\n");
    else printf("타켓 저장 인덱스 : %d \n", idx);

    return 0;
}

Reference

• 윤성우의 열혈 자료구조
• Computer Systems : A Programmer’s Perspective